第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. (2024 日照市中考)如图,在菱形 ABCD 中,AB= 2,∠B= 120°,点 O 是对角线 AC 的中点,以点 O 为圆心,OA 长为半径作圆心角为 60°的扇形 OEF,点 D 在扇形 OEF 内,则图中阴影部分的面积为(

A.$\frac{\pi}{2}-\frac{\sqrt{3}}{4}$
B.$\pi-\frac{\sqrt{3}}{4}$
C.$\frac{\pi}{2}-\frac{1}{4}$
D.无法确定
A
)
A.$\frac{\pi}{2}-\frac{\sqrt{3}}{4}$
B.$\pi-\frac{\sqrt{3}}{4}$
C.$\frac{\pi}{2}-\frac{1}{4}$
D.无法确定
答案:
A
2. 如图,同一个圆中的两条弦 AB,CD 相交于点 E. 若∠AEC= 120°,AC= 4,则$\overset{\frown}{AD}与\overset{\frown}{BC}$长度之和的最小值为(
A.4π
B.2π
C.$\frac{4}{3}\pi$
D.$\frac{2}{3}\pi$
C
)A.4π
B.2π
C.$\frac{4}{3}\pi$
D.$\frac{2}{3}\pi$
答案:
C 提示:记弦$AB$,$CD$所在的圆为$\odot O$,连接$OA$,$OB$,$OC$,$OD$。易知$\angle ACD = \frac{1}{2}\angle AOD$,$\angle BAC = \frac{1}{2}\angle BOC$,所以$\angle AOD + \angle BOC = 2(\angle ACD + \angle BAC)=2(180^{\circ}-\angle AEC)=120^{\circ}$。由三角形的三边关系,得$OA + OC\geq AC$,即$2OA\geq AC$,$OA\geq\frac{1}{2}AC$。当$A$,$O$,$C$三点共线时,等号成立。此时$\odot O$的半径最小,最小值为$\frac{1}{2}AC = 2$,$\widehat{AD}$与$\widehat{BC}$长度之和最小,最小值为$\frac{120^{\circ}×\pi×2}{180^{\circ}}=\frac{4}{3}\pi$。
3. 如图,在△ABC 中,AB= 5,AC= 3,BC= 4,将△ABC 绕点 A 按逆时针方向旋转 40°得到△ADE,点 B 经过的路径为$\overset{\frown}{BD}$,则图中阴影部分的面积为
$\frac{25\pi}{9}$
.
答案:
$\frac{25\pi}{9}$ 提示:$S_{阴影}=S_{\triangle ADE}+S_{扇形BAD}-S_{\triangle ABC}=S_{扇形BAD}=\frac{40^{\circ}×\pi×5^2}{360^{\circ}}=\frac{25\pi}{9}$。
4. (2024 兰州市中考)“轮动发石车”是我国古代的一种投石工具,在春秋战国时期被广泛应用,图 1 是陈列在展览馆的仿真模型. 图 2 是模型驱动部分的示意图,其中⊙M,⊙N 的半径分别是 1 cm 和 10 cm,当⊙M 顺时针转动 3 周时,⊙N 上的点 P 随之旋转$n^{\circ}$,则$n= $
108
.
答案:
108 提示:因为$\odot M$的周长为$2\pi\ cm$,所以$\odot M$顺时针转动$3$周时,点$P$移动的弧长为$6\pi\ cm$,所以$6\pi=\frac{n\pi×10}{180^{\circ}}$,解得$n = 108$。
5. 已知$AB= 2\sqrt{3}$,C 是平面内一个动点,$60^{\circ}\leq\angle ACB\leq120^{\circ}$,则满足条件的点 C 所在区域的面积是___.
答案:
$\frac{8\pi}{3}+4\sqrt{3}$ 提示:以$AB$为边,分别向上、向下作等边三角形,分别作出这两个等边三角形的外接圆,如图所示,由圆周角的知识可知,点$C$所在区域为图中阴影部分。设上面的等边三角形外接圆的圆心为$O$,则由圆周角定理可知,$\angle AOB = 120^{\circ}$。因为$AB = 2\sqrt{3}$,所以易得$\odot O$的半径为$2$。又易得$S_{\triangle AOB}=\frac{1}{2}×2\sqrt{3}×1=\sqrt{3}$,$S_{扇形OAB}=\frac{120^{\circ}×\pi×2^2}{360^{\circ}}=\frac{4\pi}{3}$,所以$S_2=\frac{4\pi}{3}-\sqrt{3}$。因为上、下两圆为等圆,所以$S_1=S_{\odot O}-2S_2=4\pi-2×(\frac{4\pi}{3}-\sqrt{3})=\frac{4\pi}{3}+2\sqrt{3}$。所以满足条件的点$C$所在区域的面积是$2S_1=\frac{8\pi}{3}+4\sqrt{3}$。

$\frac{8\pi}{3}+4\sqrt{3}$ 提示:以$AB$为边,分别向上、向下作等边三角形,分别作出这两个等边三角形的外接圆,如图所示,由圆周角的知识可知,点$C$所在区域为图中阴影部分。设上面的等边三角形外接圆的圆心为$O$,则由圆周角定理可知,$\angle AOB = 120^{\circ}$。因为$AB = 2\sqrt{3}$,所以易得$\odot O$的半径为$2$。又易得$S_{\triangle AOB}=\frac{1}{2}×2\sqrt{3}×1=\sqrt{3}$,$S_{扇形OAB}=\frac{120^{\circ}×\pi×2^2}{360^{\circ}}=\frac{4\pi}{3}$,所以$S_2=\frac{4\pi}{3}-\sqrt{3}$。因为上、下两圆为等圆,所以$S_1=S_{\odot O}-2S_2=4\pi-2×(\frac{4\pi}{3}-\sqrt{3})=\frac{4\pi}{3}+2\sqrt{3}$。所以满足条件的点$C$所在区域的面积是$2S_1=\frac{8\pi}{3}+4\sqrt{3}$。

6. 【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?(以下作图均不写作法,但需保留作图痕迹)
【初步尝试】如图 1,已知扇形 OAB,请你用圆规和无刻度的直尺过圆心 O 作一条直线,使扇形的面积被这条直线平分.
【问题联想】如图 2,已知线段 MN,请你用圆规和无刻度的直尺作一个以 MN 为斜边的等腰直角三角形 MNP.
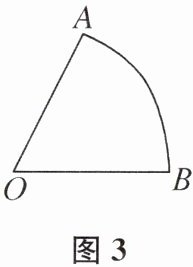
【问题再解】如图 3,已知扇形 OAB,请你用圆规和无刻度的直尺作一条以点 O 为圆心的圆弧,使扇形的面积被这条圆弧平分.
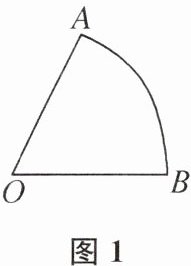

【初步尝试】如图 1,已知扇形 OAB,请你用圆规和无刻度的直尺过圆心 O 作一条直线,使扇形的面积被这条直线平分.
【问题联想】如图 2,已知线段 MN,请你用圆规和无刻度的直尺作一个以 MN 为斜边的等腰直角三角形 MNP.
【问题再解】如图 3,已知扇形 OAB,请你用圆规和无刻度的直尺作一条以点 O 为圆心的圆弧,使扇形的面积被这条圆弧平分.



答案:
解:[初步尝试][问题联想][问题再解]如图1、图2、图3所示。
提示:关于图3,由[问题联想]的结论可知,$\triangle OAD$是等腰直角三角形,所以$\frac{OA}{OE}=\frac{OA}{OD}=\sqrt{2}$。所以$\frac{S_{扇形OAB}}{S_{扇形OEF}}=\frac{\frac{n\pi\cdot OA^2}{360}}{\frac{n\pi\cdot OE^2}{360}}=\frac{OA^2}{OE^2}=2$。



解:[初步尝试][问题联想][问题再解]如图1、图2、图3所示。
提示:关于图3,由[问题联想]的结论可知,$\triangle OAD$是等腰直角三角形,所以$\frac{OA}{OE}=\frac{OA}{OD}=\sqrt{2}$。所以$\frac{S_{扇形OAB}}{S_{扇形OEF}}=\frac{\frac{n\pi\cdot OA^2}{360}}{\frac{n\pi\cdot OE^2}{360}}=\frac{OA^2}{OE^2}=2$。



查看更多完整答案,请扫码查看


