第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 有一组数据:$x_{1},x_{2},x_{3},…,x_{n}$,$(x_{1}\leqslant x_{2}\leqslant x_{3}…\leqslant\leqslant x_{n})$,它们的算术平均值为 10. 若去掉其中最大的$x_{n}$,余下数据的算术平均值为 9,则$x_{n}$关于 n 的表达式为
$x_{n}=n+9$
.
答案:
$x_{n}=n+9$ 提示:由题意知$(x_{1}+x_{2}+x_{3}+\cdots+x_{n-1})÷(n-1)=9$,所以$x_{1}+x_{2}+x_{3}+\cdots+x_{n-1}=9(n-1)$.又因为$(x_{1}+x_{2}+x_{3}+\cdots+x_{n})÷ n=10$,所以$x_{1}+x_{2}+x_{3}+\cdots+x_{n}=10n$,所以$x_{n}=10n-9(n-1)=n+9$.
2. 由 0,0,1,2,3 五个数字可以组成许多不同的五位数,所有这些五位数的平均数为
21111
.
答案:
21 111 提示:以1为开头的五位数,后四位数一共有$4×3=12$种方法,其中在每一位上,2和3各出现3次,所以1为开头的五位数的和为$10\ 000×12+(2+3)×3\ 333=136\ 665$,同样的,以2为开头的五位数的和为$20\ 000×12+(1+3)×3\ 333=253\ 332$,以3为开头的五位数的和为$30\ 000×12+(2+1)×3\ 333=369\ 999$,所以这些五位数的平均数为$(136\ 665+253\ 332+369\ 999)÷(4×3×3)=759\ 996÷36=21\ 111$.
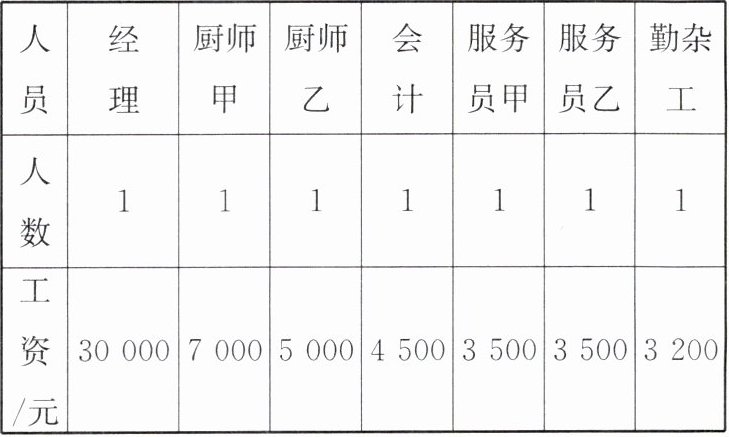
3. 某餐厅共有 7 名员工,所有员工的工资情况如下表所示:
回答下列问题:
(1)餐厅所有员工的平均工资是多少元?
(2)计算出的平均工资能否反映该餐厅员工工资的一般水平?
(3)去掉经理的工资后,其他员工的平均工资是多少元?是否能反映该餐厅员工工资的一般水平?
(4)根据以上计算,从统计的观点看,你对(2)(3)的结果有什么看法?

回答下列问题:
(1)餐厅所有员工的平均工资是多少元?
(2)计算出的平均工资能否反映该餐厅员工工资的一般水平?
(3)去掉经理的工资后,其他员工的平均工资是多少元?是否能反映该餐厅员工工资的一般水平?
(4)根据以上计算,从统计的观点看,你对(2)(3)的结果有什么看法?
答案:
解:
(1)餐厅所有员工的平均工资为$(30\ 000+7\ 000+5\ 000+4\ 500+3\ 500+3\ 500+3\ 200)÷7=8\ 100(\text{元})$.
(2)不能反映该餐厅员工工资的一般水平.
(3)去掉经理的工资后,其他员工的平均工资为$(7\ 000+5\ 000+4\ 500+3\ 500+3\ 500+3\ 200)÷6=4\ 450(\text{元})$.能反映该餐厅员工工资的一般水平.
(4)从本题的计算结果可知,个别特殊值对平均数具有很大的影响.
(1)餐厅所有员工的平均工资为$(30\ 000+7\ 000+5\ 000+4\ 500+3\ 500+3\ 500+3\ 200)÷7=8\ 100(\text{元})$.
(2)不能反映该餐厅员工工资的一般水平.
(3)去掉经理的工资后,其他员工的平均工资为$(7\ 000+5\ 000+4\ 500+3\ 500+3\ 500+3\ 200)÷6=4\ 450(\text{元})$.能反映该餐厅员工工资的一般水平.
(4)从本题的计算结果可知,个别特殊值对平均数具有很大的影响.
4. 某校团支部组建了 A(党史宣讲),B(歌曲演唱),C(校刊编撰),D(诗歌创作)四个小组,团支部将各组人数情况绘制成了如下统计图表(不完整).
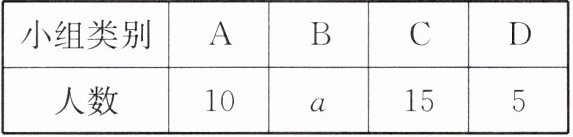
各组参加人数情况统计表
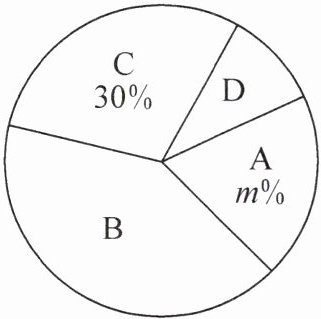
各组参加人数情况的扇形统计图
请根据统计图表中的信息,解答下列问题:
(1)求 a 和 m 的值.
(2)求扇形统计图中 D 所对应的圆心角度数.
(3)若在某一周各小组平均每人参与活动的时间情况如下表:
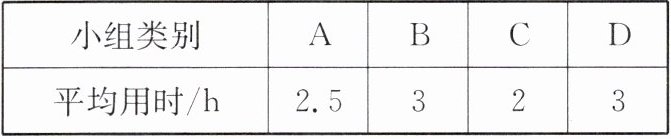
求这一周四个小组所有成员平均每人参与活动的时间.
各组参加人数情况统计表

各组参加人数情况的扇形统计图

请根据统计图表中的信息,解答下列问题:
(1)求 a 和 m 的值.
(2)求扇形统计图中 D 所对应的圆心角度数.
(3)若在某一周各小组平均每人参与活动的时间情况如下表:

求这一周四个小组所有成员平均每人参与活动的时间.
答案:
解:
(1)总参加人数为$15÷30\%=50$,则$a=50-10-15-5=20$.因为$m\%=\frac{10}{50}×100\%=20\%$,所以$m=20$.
(2)$\frac{5}{50}×360^{\circ}=36^{\circ}$.答:扇形统计图中D所对应的圆心角度数是$36^{\circ}$.
(3)$\overline{x}=\frac{1}{50}×(10×2.5+20×3+15×2+5×3)=2.6(\text{h})$.答:这一周四个小组所有成员平均每人参与活动的时间是2.6 h.
(1)总参加人数为$15÷30\%=50$,则$a=50-10-15-5=20$.因为$m\%=\frac{10}{50}×100\%=20\%$,所以$m=20$.
(2)$\frac{5}{50}×360^{\circ}=36^{\circ}$.答:扇形统计图中D所对应的圆心角度数是$36^{\circ}$.
(3)$\overline{x}=\frac{1}{50}×(10×2.5+20×3+15×2+5×3)=2.6(\text{h})$.答:这一周四个小组所有成员平均每人参与活动的时间是2.6 h.
查看更多完整答案,请扫码查看


