《2025年小题狂做九年级数学上册苏科版提优版》

1. 某渔民捕捞了一些春虾,从中抽取了 10 尾春虾,其长度(单位：cm)如下：8.8,8.6,9.1,9.2,8.9,8.9,9.3,8.9,9.4,8.9. 利用计算器计算被抽取的这组数据的方差是 (B)
$A. 0.72 cm^2$

$B. 0.054 cm^2$

$C. 0.045 cm^2$

$D. 0.076 cm^2$

答案： B

2. 某工厂为了选拔 1 名车工参加加工直径为 10 mm 的精密零件的技术比赛,随机抽取甲、乙两名车工加工的 5 个零件,测得的结果如下表. 请你用计算器比较$s_{甲}^{2},s_{乙}^{2}$的大小 (A)
A.$s_{甲}^{2}＞s_{乙}^{2}$
B.$s_{甲}^{2}= s_{乙}^{2}$
C.$s_{甲}^{2}＜s_{乙}^{2}$
D.$s_{甲}^{2}\leq s_{乙}^{2}$

答案： A

3. 在一次爱心捐款活动中,某班 50 名学生积极捐款,其中 5 人每人捐款 5 元,8 人每人捐款 15 元,12 人每人捐款 25 元,18 人每人捐款 35 元,7 人每人捐款 45 元,则该班 50 名学生捐款金额的方差为140.16元$^2.$

答案： 140.16

4. 给定一组数据如下：1,1,4,4,4,7,7.
(1)请你估计一下这组数据的平均数、方差各是多少.
(2)用计算器计算这组数据的平均数、方差,与你的估计值进行比较,你的估计是否准确？

答案： 解:
(1) 估计这组数据的平均数是 4、方差是 5.
(2)平均数为$(1+1+4+4+4+7+7)÷7=4$,方差为$\frac {1}{7}×[2×(1-4)^{2}+3×(4-4)^{2}+2×(7-4)^{2}]=5\frac {1}{7}$.与估计值进行比较,估计基本准确.

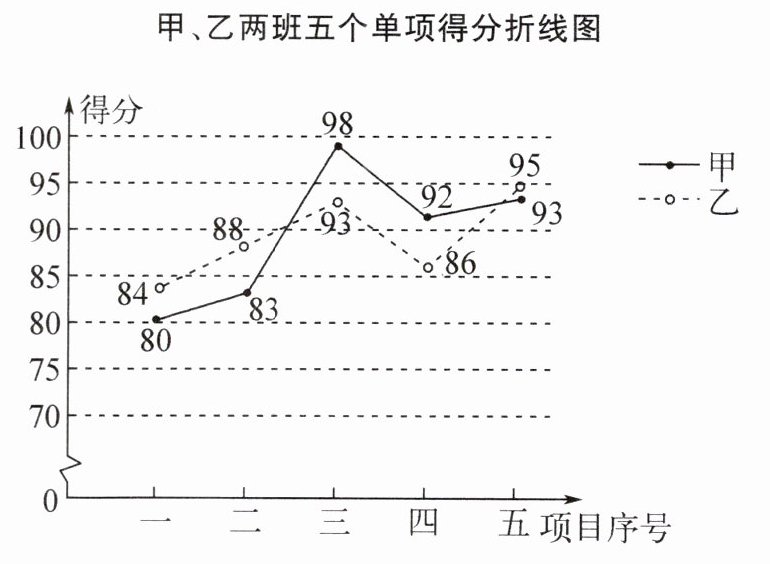
5. (2024 日照市中考)为进一步推动阳光体育运动,提高学生身体素质,今年 5 月学校举行健美操比赛,最终有甲、乙、丙三个班级进入团体决赛. 团体决赛需要分别进行五个单项比赛,计分规则如下表：
|单项比赛计分规则|五名裁判打分,去掉一个最高分和一个最低分,剩下三个有效分的平均数即为该项得分|
|团体决赛计分规则|各单项比赛得分之和为团体最终成绩,名次按团体最终成绩由高到低排序|

现将参加比赛的甲、乙、丙三个班级的得分数据进行整理、描述和分析,并绘制统计图表,部分信息如下：
甲、乙两班五个单项得分折线图

丙班五个单项得分表

根据以上信息,回答下列问题：
(1)已知丙班第二个单项比赛中,五名裁判的打分分别为 80,84,86,83,82,求丙班第二个单项的得分 m.
(2)若团体最终成绩相同,则整体发挥稳定性最好的班级排名靠前,那么获得团体比赛冠军的是______班(填“甲”“乙”或“丙”).
(1)83
(2)乙

答案： 解:
(1) 去掉最高分 86 分,最低分 80 分后,$m=\frac {1}{3}×(84+83+82)=83$(分),所以丙班第二个单项得分为 83 分.
(2) 乙 提示:甲班团体最终成绩为$80+83+98+92+93=446$(分),用计算器计算甲班五个单项得分的方差为 44.56 分²;乙班团体最终成绩为$84+88+93+86+95=446$(分),乙班的方差为17.36 分²;丙班团体最终成绩为$78+83+94+90+92=437$(分).$437＜446,44.56＞17.36$,所以乙班获得团体比赛冠军.