第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. (2024 山西省中考)如图,已知△ABC,以AB 为直径的⊙O 交 BC 于点 D,与 AC 相切于点 A,连接 OD. 若∠AOD= 80°,则∠C 的度数为(
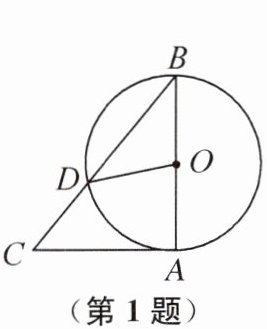
A.30°
B.40°
C.45°
D.50°
D
)
A.30°
B.40°
C.45°
D.50°
答案:
D
2. (2024 福建省中考)如图,已知点 A,B 在⊙O 上,∠AOB= 72°,直线 MN 与⊙O 相切,切点为 C,且 C 为$\overset{\frown}{AB}$的中点,则∠ACM 的度数为(
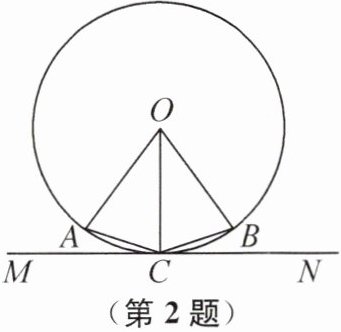
A.18°
B.30°
C.36°
D.72°
A
)
A.18°
B.30°
C.36°
D.72°
答案:
A
3. 如图,BC 为⊙O 的直径,弦 AD⊥BC 于点 E,直线 l 切⊙O 于点 C,延长 OD 交 l 于点 F. 若 AE= 2,∠ABC= 22.5°,则 CF的长为(
A.2
B.$2\sqrt{2}$
C.$2\sqrt{3}$
D.4
B
)A.2
B.$2\sqrt{2}$
C.$2\sqrt{3}$
D.4
答案:
B
4. 如图,在矩形 ABCD 中,AB= 8,AD= 12,过 A,D 两点的⊙O 与边 BC 相切于点 E,则⊙O 的半径为(
A.5
B.5.25
C.6
D.6.25
D
)A.5
B.5.25
C.6
D.6.25
答案:
D 提示:连接 EO 并延长,交 AD 于点 F,连接 OA.因为 BC 是$\odot O$的切线,所以$OE⊥BC$,所以$∠OEC=90^{\circ }$.因为四边形 ABCD 是矩形,所以$∠C=∠D=90^{\circ }$,所以四边形 CDFE 是矩形,所以$EF=CD=AB=8,OF⊥AD$,所以$AF=\frac {1}{2}AD=6$.设$\odot O$的半径为x,则$OF=EF - OE=8 - x$.在$Rt△OAF$中,由勾股定理,得$OF^{2}+AF^{2}=OA^{2}$,即$(8 - x)^{2}+6^{2}=x^{2}$,解得$x = 6.25$.所以$\odot O$的半径为 6.25.
5. 如图,在平面直角坐标系 xOy 中,直线 AB经过点 A(4,0),B(0,4),⊙O 的半径为2(O 为坐标原点),P 是直线 AB 上的一动点,过点 P 作⊙O 的一条切线 PQ,Q 为切点,则线段 PQ 长的最小值为(
A.$\sqrt{7}$
B.$2\sqrt{2}-1$
C.2
D.$3\sqrt{2}$
C
)A.$\sqrt{7}$
B.$2\sqrt{2}-1$
C.2
D.$3\sqrt{2}$
答案:
C 提示:连接 OP,OQ.因为点$A(4,0),B(0,4)$,所以$OA = OB = 4$,因为$∠AOB = 90^{\circ }$,所以$△AOB$为等腰直角三角形,所以$AB = \sqrt{OA^{2}+OB^{2}} = 4\sqrt{2}$.因为 PQ 是$\odot O$的切线,所以$OQ⊥PQ$.在$Rt△OPQ$中,由勾股定理,得$PQ = \sqrt{OP^{2}-OQ^{2}} = \sqrt{OP^{2}-4}$,所以当 OP 的长最小时,PQ 的长最小,由题意可知,当$OP⊥AB$时,OP 的长最小,此时易求$OP = \frac{1}{2}AB = 2\sqrt{2},PQ = \sqrt{OP^{2}-4} = 2$.所以线段 PQ 长的最小值为 2.
6. (2024 徐州市中考)如图,AB 是⊙O 的直径,点 C 在 AB 的延长线上,CD 与⊙O 相切于点 D,若∠C= 20°,则∠CAD=
35
°.
答案:
35
7. 如图是某个球放进盒子内的截面图,球的一部分露出盒子外. 已知⊙O 交矩形 ABCD 的边 AD 于点 E,F,AB= EF= 2,则球的半径为______
$\frac{5}{4}$
.
答案:
$\frac{5}{4}$
8. 如图,直线 AB 与⊙O 相切于点 A,AC,CD 是⊙O 的两条弦,且 CD//AB. 若⊙O 的半径为 2.5,CD= 4,则弦 AC 的长为______
$2\sqrt{5}$
.
答案:
$2\sqrt{5}$ 提示:连接 AO 并延长,交 CD 于点 E,连接 OC.因为 AB 与$\odot O$相切,所以$OA⊥AB$.因为$CD// AB$,所以$OA⊥CD$,所以$CE = DE = 2$.在$Rt△OEC$中,由勾股定理,得$OE = \sqrt{OC^{2}-CE^{2}} = \frac{3}{2}$,所以$AE = OE + OA = 4$.在$Rt△AEC$中,由勾股定理,得$AC = \sqrt{AE^{2}+CE^{2}} = 2\sqrt{5}$.
1. 如图,⊙O 的半径为 2,点 O 到直线 l 的距离为 3,P 是直线 l 上的一个动点,PB 切⊙O 于点 B,则 PB 的最小值是(
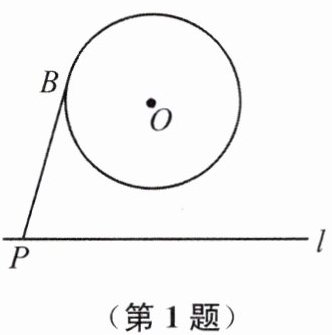
A.$\sqrt{13}$
B.$\sqrt{5}$
C.3
D.2
B
)
A.$\sqrt{13}$
B.$\sqrt{5}$
C.3
D.2
答案:
B
查看更多完整答案,请扫码查看


