第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图,已知$\odot O$的半径为 4,M 是$\odot O$内一定点,且$OM= 2$,则过点 M 的所有弦中,弦长是整数的有(
A.1条
B.2条
C.3条
D.4条
C
)A.1条
B.2条
C.3条
D.4条
答案:
C
2. 如图,在$\odot O$中,分别将$\widehat {AB}和\widehat {CD}$沿两条互相平行的弦 AB 和弦 CD 折叠,折叠后的弧均过圆心.若$\odot O$的半径为 4,则四边形 ABCD 的面积是(
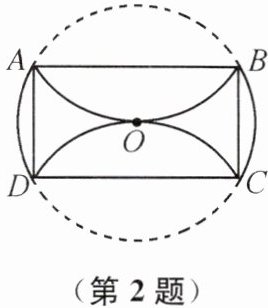
A.8
B.$16\sqrt {3}$
C.32
D.$32\sqrt {3}$
B
)
A.8
B.$16\sqrt {3}$
C.32
D.$32\sqrt {3}$
答案:
B
3. 如图,$\odot O$的半径 OD 垂直于弦 AB,垂足为 C,连接 AO 并延长交$\odot O$于点 E,连接 BE,CE. 若$AB= 8,CD= 2$,则$\triangle BCE$的面积为(
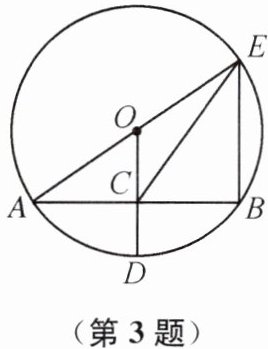
A.12
B.15
C.16
D.18
A
)
A.12
B.15
C.16
D.18
答案:
A
4.(2024 南京市鼓楼区期中)如图,$\odot O$的半径为 5,$OP= 1$,若将$\odot O$沿某条弦所在的直线翻折,翻折后的弧恰好经过点 P,则这条弦的长度 a 的范围是______
$8\leqslant a\leqslant 2\sqrt{21}$
.
答案:
$8\leqslant a\leqslant 2\sqrt{21}$ 提示:过点P作⊙O的直径CE.由垂径定理知,当弦AB垂直平分CP时,弦AB最短,当弦AB垂直平分PE时,弦AB最长.如图1,连接OA.因为⊙O的半径为5,OP=1,所以CP=OC - OP=4.由翻折易得CD=PD=$\frac{1}{2}$CP=2,所以OD=3,在Rt△OAD中,AD=$\sqrt{OA^2 - OD^2}$=4,所以a=AB=2AD=8.如图2,连接OA.因为⊙O的半径为5,OP=1,所以PE=OE + OP=6.由翻折易得,ED=PD=$\frac{1}{2}$PE=3,所以OD=2,在Rt△OAD中,AD=$\sqrt{OA^2 - OD^2}$=$\sqrt{21}$,所以a=AB=2AD=$2\sqrt{21}$.所以这条弦的长度a的范围是$8\leqslant a\leqslant 2\sqrt{21}$.
5.(2024 常州市期中)如图1是一款轴对称的"磁悬浮地漏"无水时的示意图,它由一个圆弧形密封盖$\widehat {MN}$与两个磁体组成(下侧磁体固定不动),连接杆 EF 与地面 BD 垂直,排水口$CD= 24\sqrt {3}mm$,密封盖最高点 E 到地面的距离为 6 mm,整个地漏的高度$EG= 75mm$(G 为磁体底部中点),密封盖$\widehat {MN}$所在圆的半径为
39
mm;当有水时如图2所示,密封盖下移排水,当密封盖下沉至最低处时,点$M'$恰好落在 BG 中点处,若点$M'到E'F'$的距离为 36 mm,则密封盖下沉的最大距离为16.5
mm.
答案:
39 16.5 提示:如图1,设MN所在圆的圆心为点O,连接CD交EF于点H,连接OD.设OH=x mm,因为最高点E到地面的距离为6 mm,所以OE=(6 + x)mm.因为CD=$24\sqrt{3}$ mm,所以DH=$12\sqrt{3}$ mm,所以在Rt△OHD中,OD=$\sqrt{x^2+(12\sqrt{3})^2}$mm,因为OE=OD,所以6 + x=$\sqrt{x^2+(12\sqrt{3})^2}$,解得x=33,所以OE=39 mm.如图2,过点A'作M'P'⊥E'G于点P',延长GE',交AB于点Q',过点M'作M'Z⊥AB于点Z,易证M'Z//E'G.又因为M'为BG的中点,易得Z是BQ'的中点,所以M'Z为△GQ'B的中位线,所以M'Z=$\frac{1}{2}$GQ',因为EG=75 mm,EQ'=6 mm,所以GQ'=69 mm,所以M'Z=$\frac{1}{2}$GQ'=34.5 mm.在图1中,过点M作MJ⊥EF于点J,连接OM.因为点M'到E'F'的距离为36 mm,所以MJ=M'P'=36 mm.因为OM=OE=39 mm,由勾股定理,得OJ=$\sqrt{OM^2 - MJ^2}$=$\sqrt{39^2 - 36^2}$=15(mm),所以移动前点M到地面的距离为JH=39 - 15 - 6=18(mm),所以密封盖下沉的最大距离为M'Z - JH=34.5 - 18=16.5(mm).
6. 如图,M 为$\odot O$内任意一点,AB 为过点 M 且和 OM 垂直的一条弦,CD 为过点 M 的任意一条弦(不与 AB 重合).
(1) 求证:$AB\lt CD.$
(2) 在过点 M 的所有弦中,有没有最长的弦?
(3) 如果过点 M 的所有弦中,最长的弦是 EF,最短的弦是 GH,且$EF= 26,$$GH= 24$,求 OM 的长度.
(1) 求证:$AB\lt CD.$
证明:连接OA,OD,过点O作ON⊥CD于点N.所以DN=$\frac{1}{2}$CD,OM>ON.因为OM⊥AB,所以AM=$\frac{1}{2}$AB.由勾股定理,得AM²=OA² - OM²,DN²=OD² - ON².因为OA=OD,OM>ON,所以AM²<DN²,所以AM<DN,所以AB<CD.
(2) 在过点 M 的所有弦中,有没有最长的弦?
有
(填"有"或"没有").有没有最短的弦?有
(填"有"或"没有").如果有,最长的弦与 OM 的位置关系为重合
,最短的弦与 OM 的位置关系为垂直
.(3) 如果过点 M 的所有弦中,最长的弦是 EF,最短的弦是 GH,且$EF= 26,$$GH= 24$,求 OM 的长度.
解:如图,连接OG.由题意,得EF⊥GH,EF是⊙O的直径,OG=13,GM=12,所以OM=$\sqrt{OG^2 - GM^2}$=$\sqrt{13^2 - 12^2}$=5.
答案:
(1)证明:连接OA,OD,过点O作ON⊥CD于点N.所以DN=$\frac{1}{2}$CD,OM>ON.因为OM⊥AB,所以AM=$\frac{1}{2}$AB.由勾股定理,得AM²=OA² - OM²,DN²=OD² - ON².因为OA=OD,OM>ON,所以AM²<DN²,所以AM<DN,所以AB<CD.(2)有 有 重合 垂直 提示:由
(1)可知,在过点M的所有弦中,AB是最短的一条.因为CD为过点M的任意一条弦,连接OC,OD,所以OC + OD≥CD,OC + OD的长等于直径长,即在过点M的所有弦中,与弦AB垂直的直径是最长的弦.(3)解:如图,连接OG.由题意,得EF⊥GH,EF是⊙O的直径,OG=13,GM=12,所以OM=$\sqrt{OG^2 - GM^2}$=$\sqrt{13^2 - 12^2}$=5.
(1)可知,在过点M的所有弦中,AB是最短的一条.因为CD为过点M的任意一条弦,连接OC,OD,所以OC + OD≥CD,OC + OD的长等于直径长,即在过点M的所有弦中,与弦AB垂直的直径是最长的弦.(3)解:如图,连接OG.由题意,得EF⊥GH,EF是⊙O的直径,OG=13,GM=12,所以OM=$\sqrt{OG^2 - GM^2}$=$\sqrt{13^2 - 12^2}$=5.
查看更多完整答案,请扫码查看


