第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
2. 如图,△ABC 是等腰直角三角形,AC= BC= 2,以斜边 AB 上的点 O 为圆心的圆分别与 AC,BC 相切于点 D,E,与 AB 交于点 G,H,且 DG 的延长线和 CB 的延长线交于点 F,则 CF 的长为(
A.1
B.$2\sqrt{2}+1$
C.$1+\sqrt{2}$
D.$2+\sqrt{2}$
C
)A.1
B.$2\sqrt{2}+1$
C.$1+\sqrt{2}$
D.$2+\sqrt{2}$
答案:
C 提示:连接 CO,DO,EO.因为 AC,BC 是$\odot O$的切线,所以$OD⊥AC,OE⊥BC$.因为$△ABC$是等腰直角三角形,$AC = BC = 2$,所以$AB = 2\sqrt{2},∠A = 45^{\circ }$.所以$△ADO$是等腰直角三角形,所以$AD = OD$.因为$∠C = ∠ODC = ∠OEC = 90^{\circ }$,所以四边形 CDOE 是矩形.因为$OD = OE$,所以矩形 CDOE 是正方形.所以$OD = DC$.因为$AD = OD$,所以$AD = DC = \frac{1}{2}AC = 1$.所以$△COD$是等腰直角三角形,所以$∠AOD + ∠COD = 90^{\circ }$,所以$CO⊥AB$,所以 O 是 AB 的中点.所以$OA = OB = \frac{1}{2}AB = \sqrt{2}$.因为$DO// BC$,所以$∠F = ∠ODG$.因为$OD = OG$,所以$∠ODG = ∠OGD$.因为$∠OGD = ∠FGB$,所以$∠FGB = ∠F$.所以$BG = BF = \sqrt{2}-1$,所以$CF = CB + BF = 2 + \sqrt{2}-1 = 1 + \sqrt{2}$.
3. 如图,在平面直角坐标系 xOy 中,点 P 在第一象限,⊙P 与 x 轴、y 轴都相切,且经过矩形 AOBC 的顶点 C,与 BC 相交于点 D. 若⊙P 的半径为 5,点 A 的坐标是(0,8),则点 D 的坐标是(
A.(9,2)
B.(9,3)
C.(10,2)
D.(10,3)
(9,2)
)A.(9,2)
B.(9,3)
C.(10,2)
D.(10,3)
答案:
A 提示:设$\odot O$与x轴、y轴的切点分别是F,E,连接 PE,PF,PD,延长 EP 与 CD 交于点 G.易证四边形 PEOF 为正方形,所以$OE = PF = PE = OF = 5$.因为点$A(0,8)$,所以$OA = 8$,所以$AE = OA - OE = 3$.因为四边形 AOBC 为矩形,所以$BC = OA = 8$.易证四边形 AEGC、四边形 OEGB 均为矩形,所以$CG = AE = 3,EG = OB$.因为$PE⊥AO,BC// OA$,所以$PG⊥CD$,所以$DG = CG = 3$,所以$BD = BC - CG - DG = 2$.因为$PD = 5,DG = 3$,所以$PG = 4$,所以$OB = EG = PE + PG = 9$,所以点$D(9,2)$.
4. 如图,在△ABC 中,AB= 10,AC= 8,BC= 6,以边 AB 的中点 O 为圆心,作半圆与 AC 相切,P,Q 分别是边 BC 和半圆上的动点,连接 PQ,则 PQ 长的最大值与最小值的和是______
9
.
答案:
9 提示:如图,过点 O 作$OP_{1}⊥BC$于点$P_{1}$,交半圆于点$Q_{1}$.设半圆与 OA 相交于点$Q_{2}$,连接 OC,$OP,OQ$.设半圆与 AC 相切于点 E,连接 OE,则$OE⊥AC$.因为$OQ + PQ≥OP≥OP_{1}$,即$PQ≥OP - OQ≥OP_{1}-OQ_{1}=P_{1}Q_{1}$.所以当 O,Q,P 三点依次共线且点 P 与点$P_{1}$重合时,PQ 长有最小值,为$P_{1}Q_{1}$的长;因为$PQ≤OP + OQ$,所以当 Q,O,P 三点依次共线,即点 Q 运动到点$Q_{2}$,点 P 运动到点 B 时,PQ 长有最大值,为$BQ_{2}$的长.因为$AB = 10,AC = 8,BC = 6$,所以$AB^{2}=AC^{2}+BC^{2}$,所以$△ABC$为直角三角形.因为$OA = OB$,所以$OC = \frac{1}{2}AB = OA = OB$.因为$OE⊥AC$,所以$AE = CE$,所以$OE = \frac{1}{2}BC = 3$.因为$OP_{1}⊥BC$,所以$P_{1}C = P_{1}B$,所以$OP_{1} = \frac{1}{2}AC = 4$.所以 PQ 长的最小值$P_{1}Q_{1}=OP_{1}-OQ_{1}=OP_{1}-OE = 1$,最大值$BQ_{2}=OQ_{2}+OB = OE + OB = 8$.所以 PQ 长的最大值与最小值的和是 9.
5. (2024 天津市中考)已知在△AOB 中,∠ABO= 30°,AB 为⊙O 的弦,直线 MN 与⊙O 相切于点 C.
(1)如图 1,若 AB//MN,直径 CE 与 AB 相交于点 D,求∠AOB 和∠BCE 的大小;
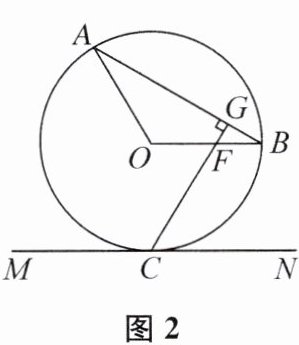
(2)如图 2,若 OB//MN,CG⊥AB,垂足为 G,CG 与 OB 相交于点 F,OA= 3,求线段 OF 的长.
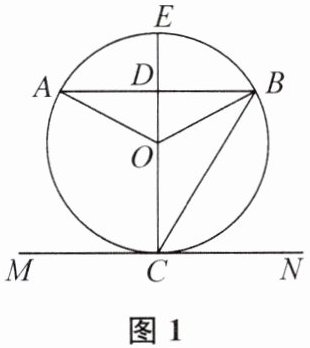
(1)如图 1,若 AB//MN,直径 CE 与 AB 相交于点 D,求∠AOB 和∠BCE 的大小;
(2)如图 2,若 OB//MN,CG⊥AB,垂足为 G,CG 与 OB 相交于点 F,OA= 3,求线段 OF 的长.


答案:
(1)因为$OA = OB$,所以$∠A = ∠ABO$.因为$∠A + ∠ABO + ∠AOB = 180^{\circ },∠ABO = 30^{\circ }$,所以$∠AOB = 180^{\circ }-2∠ABO = 120^{\circ }$.因为直线 MN 与$\odot O$相切于点 C,CE 为$\odot O$的直径,所以$∠ECN = 90^{\circ }$.因为$AB// MN$,所以$∠CDB = ∠ECN = 90^{\circ }$,所以$∠BOE = 180^{\circ }-∠CDB - ∠ABO = 60^{\circ }$.因为$∠BCE = \frac{1}{2}∠BOE$,所以$∠BCE = 30^{\circ }$.
(2)如图,连接 OC.同
(1),得$∠COB = 90^{\circ }$.因为$CG⊥AB$,所以$∠FGB = 90^{\circ }$.因为$∠ABO = 30^{\circ }$,所以$∠BFG = 90^{\circ }-∠ABO = 60^{\circ }$,所以$∠CFO = ∠BFG = 60^{\circ }$.在$Rt△COF$中,$OC = OA = 3,∠CFO = 60^{\circ }$,所以$CF = 2OF$,由勾股定理,得$OF^{2}+OC^{2}=CF^{2}$,即$OF^{2}+3^{2}=(2OF)^{2}$,所以$OF = \sqrt{3}$.
(1)因为$OA = OB$,所以$∠A = ∠ABO$.因为$∠A + ∠ABO + ∠AOB = 180^{\circ },∠ABO = 30^{\circ }$,所以$∠AOB = 180^{\circ }-2∠ABO = 120^{\circ }$.因为直线 MN 与$\odot O$相切于点 C,CE 为$\odot O$的直径,所以$∠ECN = 90^{\circ }$.因为$AB// MN$,所以$∠CDB = ∠ECN = 90^{\circ }$,所以$∠BOE = 180^{\circ }-∠CDB - ∠ABO = 60^{\circ }$.因为$∠BCE = \frac{1}{2}∠BOE$,所以$∠BCE = 30^{\circ }$.
(2)如图,连接 OC.同
(1),得$∠COB = 90^{\circ }$.因为$CG⊥AB$,所以$∠FGB = 90^{\circ }$.因为$∠ABO = 30^{\circ }$,所以$∠BFG = 90^{\circ }-∠ABO = 60^{\circ }$,所以$∠CFO = ∠BFG = 60^{\circ }$.在$Rt△COF$中,$OC = OA = 3,∠CFO = 60^{\circ }$,所以$CF = 2OF$,由勾股定理,得$OF^{2}+OC^{2}=CF^{2}$,即$OF^{2}+3^{2}=(2OF)^{2}$,所以$OF = \sqrt{3}$.
6. 如图,在△ABC 中,D 为边 BC 上的一个动点,以 CD 为直径的⊙O 交 AD 于点 E,过点 C 作 CF//AB,交⊙O 于点 F,连接 CE,EF. 已知 AC 是⊙O 的切线.
(1)求证:∠BAC= ∠CEF;
(2)若 AB= 10,AC= 6,CE= EF,求直径 CD 的长.
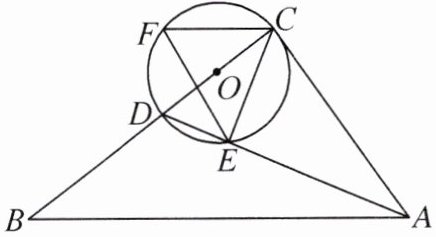
(1)求证:∠BAC= ∠CEF;
(2)若 AB= 10,AC= 6,CE= EF,求直径 CD 的长.

答案:
(1)证明:因为$CF// AB$,所以$∠B = ∠FCB$.因为$∠FCB = ∠DEF$,所以$∠B = ∠DEF$.因为 AC 是$\odot O$的切线,所以$∠ACB = 90^{\circ }$,所以$∠BAC + ∠B = 90^{\circ }$.因为 CD 是$\odot O$的直径,所以$∠CED = 90^{\circ }$,所以$∠DEF + ∠CEF = 90^{\circ }$,所以$∠BAC = ∠CEF$.
(2)解:连接 FD 并延长,交 AB 于点 G.因为$CE = EF$,所以$∠CFE = ∠ECF$.因为四边形 CEDF 为圆内接四边形,所以$∠FDE + ∠ECF = 180^{\circ }$,又因为$∠FDE + ∠ADG = 180^{\circ }$,所以$∠ADG = ∠ECF = ∠CFE$.又因为$∠CDE = ∠CFE$,所以$∠ADG = ∠CDE$.因为 CD 为$\odot O$的直径,所以$∠CFD = 90^{\circ }$.因为$CF// AB$,所以$∠AGD = ∠CFD = 90^{\circ }$,所以$∠AGD = ∠ACD$.又因为$AD = AD$,所以$△AGD\cong△ACD(AAS)$,所以$DG = CD,AC = AG = 6$.因为$∠ACB = 90^{\circ },AB = 10,AC = 6$,所以$BC = \sqrt{AB^{2}-AC^{2}} = 8$.在$Rt△BDG$中,设$CD = DG = x$,则$BD = BC - CD = 8 - x,BG = AB - AG = 10 - 6 = 4$.由勾股定理,得$BG^{2}+DG^{2}=BD^{2}$,即$4^{2}+x^{2}=(8 - x)^{2}$,解得$x = 3$,所以 CD 的长为 3.
(1)证明:因为$CF// AB$,所以$∠B = ∠FCB$.因为$∠FCB = ∠DEF$,所以$∠B = ∠DEF$.因为 AC 是$\odot O$的切线,所以$∠ACB = 90^{\circ }$,所以$∠BAC + ∠B = 90^{\circ }$.因为 CD 是$\odot O$的直径,所以$∠CED = 90^{\circ }$,所以$∠DEF + ∠CEF = 90^{\circ }$,所以$∠BAC = ∠CEF$.
(2)解:连接 FD 并延长,交 AB 于点 G.因为$CE = EF$,所以$∠CFE = ∠ECF$.因为四边形 CEDF 为圆内接四边形,所以$∠FDE + ∠ECF = 180^{\circ }$,又因为$∠FDE + ∠ADG = 180^{\circ }$,所以$∠ADG = ∠ECF = ∠CFE$.又因为$∠CDE = ∠CFE$,所以$∠ADG = ∠CDE$.因为 CD 为$\odot O$的直径,所以$∠CFD = 90^{\circ }$.因为$CF// AB$,所以$∠AGD = ∠CFD = 90^{\circ }$,所以$∠AGD = ∠ACD$.又因为$AD = AD$,所以$△AGD\cong△ACD(AAS)$,所以$DG = CD,AC = AG = 6$.因为$∠ACB = 90^{\circ },AB = 10,AC = 6$,所以$BC = \sqrt{AB^{2}-AC^{2}} = 8$.在$Rt△BDG$中,设$CD = DG = x$,则$BD = BC - CD = 8 - x,BG = AB - AG = 10 - 6 = 4$.由勾股定理,得$BG^{2}+DG^{2}=BD^{2}$,即$4^{2}+x^{2}=(8 - x)^{2}$,解得$x = 3$,所以 CD 的长为 3.
查看更多完整答案,请扫码查看


