第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图,已知AB= AC= AD,∠CBD= 2∠BDC,∠BAC= 44°,则∠CAD的度数为(
A.68°
B.88°
C.90°
D.112°
B
)A.68°
B.88°
C.90°
D.112°
答案:
B 提示:因为AB=AC=AD,所以B,C,D三点共圆,且圆心为点A.因为∠BAC=44°,所以∠BDC=22°.所以∠CAD=2∠CBD=4∠BDC=88°.
2. (2024海南省中考)如图,AD是半圆O的直径,点B,C在半圆上,且$\widehat{AB}= \widehat{BC}= \widehat{CD}$,点P在$\widehat{CD}$上,若∠PCB= 130°,则∠PBA等于( )

A.105°
B.100°
C.90°
D.70°

A.105°
B.100°
C.90°
D.70°
答案:
B 提示:如图,连接OB,OC.因为AD是半圆O 的直径,所以∠AOD=180°,因为AB=BC=CD,所以∠AOB=∠BOC=∠COD=60°.又因为OA=OB=OC,所以△AOB,△BOC均是等边三角形,所以∠ABC=120°,∠BPC=$\frac{1}{2}$∠BOC=30°.又因为∠PCB=130°,所以∠PBC=20°,所以∠PBA=∠ABC - ∠PBC=120° - 20°=100°.
B 提示:如图,连接OB,OC.因为AD是半圆O 的直径,所以∠AOD=180°,因为AB=BC=CD,所以∠AOB=∠BOC=∠COD=60°.又因为OA=OB=OC,所以△AOB,△BOC均是等边三角形,所以∠ABC=120°,∠BPC=$\frac{1}{2}$∠BOC=30°.又因为∠PCB=130°,所以∠PBC=20°,所以∠PBA=∠ABC - ∠PBC=120° - 20°=100°.

3. (2024广州市中考)如图,在⊙O中,弦AB的长为$4\sqrt{3}$,点C在⊙O上,OC⊥AB,∠ABC= 30°. 已知⊙O所在的平面内有一点P,若OP= 5,则点P与⊙O的位置关系是(
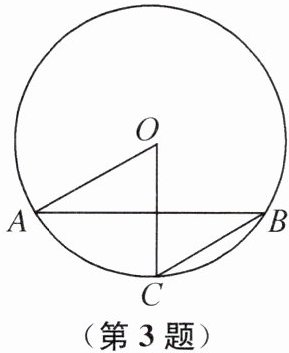
A.点P在⊙O上
B.点P在⊙O内
C.点P在⊙O外
D.无法确定
C
)
A.点P在⊙O上
B.点P在⊙O内
C.点P在⊙O外
D.无法确定
答案:
C 提示:设AB与OC交于点D.因为弦AB的长为$4\sqrt{3}$,OC⊥AB,所以AD=BD=$\frac{1}{2}$AB=$2\sqrt{3}$.因为∠ABC=30°,所以∠AOD=60°,所以∠A=30°,所以OA=2OD.设OD=x,则OA=2x,在Rt△AOD中,由勾股定理,得OD²+AD²=OA²,即$x^{2}+(2\sqrt{3})^{2}=(2x)^{2}$,解得x=2(负值已舍),所以OA=2x=4.因为OP=5,所以OP>OA,所以点P在⊙O外.
4. (2024江西省中考)如图,AB是⊙O的直径,AB= 2,点C在线段AB上运动,过点C的弦DE⊥AB,将$\widehat{DBE}$沿DE翻折交直线AB于点F,当DE的长为正整数时,线段FB的长为______.
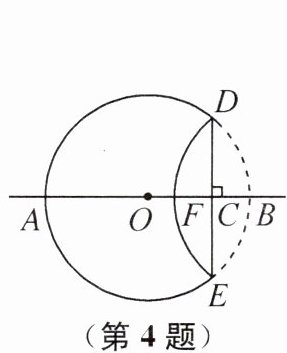

答案:
$2-\sqrt{3}$或$2+\sqrt{3}$或2 提示:因为AB为直径,DE为弦,所以DE≤AB,所以当DE的长为正整数时,DE=1或2.当DE=2时,DE为直径,因为DE⊥AB,所以此时点F与点A重合,故FB=2.当DE=1时,若点C在线段OB上,如图1,连接OD,则OD=$\frac{1}{2}$AB=1,因为DE⊥AB,所以DC=$\frac{1}{2}$DE=$\frac{1}{2}$,所以OC=$\sqrt{OD^{2}-DC^{2}}=\frac{\sqrt{3}}{2}$,所以BC=OB - OC=$\frac{2-\sqrt{3}}{2}$,所以FB=2BC=$2-\sqrt{3}$;若点C在线段OA上,如图2,连接OD,同理可得BC=$\frac{2+\sqrt{3}}{2}$,所以FB=2BC=$2+\sqrt{3}$.综上所述,线段FB的长为$2-\sqrt{3}$或$2+\sqrt{3}$或2.

$2-\sqrt{3}$或$2+\sqrt{3}$或2 提示:因为AB为直径,DE为弦,所以DE≤AB,所以当DE的长为正整数时,DE=1或2.当DE=2时,DE为直径,因为DE⊥AB,所以此时点F与点A重合,故FB=2.当DE=1时,若点C在线段OB上,如图1,连接OD,则OD=$\frac{1}{2}$AB=1,因为DE⊥AB,所以DC=$\frac{1}{2}$DE=$\frac{1}{2}$,所以OC=$\sqrt{OD^{2}-DC^{2}}=\frac{\sqrt{3}}{2}$,所以BC=OB - OC=$\frac{2-\sqrt{3}}{2}$,所以FB=2BC=$2-\sqrt{3}$;若点C在线段OA上,如图2,连接OD,同理可得BC=$\frac{2+\sqrt{3}}{2}$,所以FB=2BC=$2+\sqrt{3}$.综上所述,线段FB的长为$2-\sqrt{3}$或$2+\sqrt{3}$或2.


5. 某数学活动小组在一次活动中,对一个数学问题作如下探究:
【问题发现】如图1,AD,BD为⊙O的两条弦(AD<BD),C为$\widehat{AB}$的中点,过点C作CE⊥BD,垂足为E. 求证:BE= DE+AD.
【问题探究】小明同学的思路是:如图2,在BE上截取BF= AD,连接CA,CB,CD,CF……
请你按照小明的思路将上述问题的证明过程补充完整.
【结论运用】如图3,△ABC是⊙O的内接等边三角形,D是$\widehat{AB}$上一点,连接BD,CD,∠ACD= 45°,过点A作AE⊥CD,垂足为E. 若AB= $4\sqrt{2}$,则△BCD的周长为______.
【变式探究】如图4,若将【问题发现】中“C为$\widehat{AB}$的中点”改为“C为优弧AB的中点”,其他条件不变,上述结论“BE= DE+AD”还成立吗?若成立,请说明理由;若不成立,请写出BE,AD,DE之间的新等量关系,并加以证明.
【问题发现】如图1,AD,BD为⊙O的两条弦(AD<BD),C为$\widehat{AB}$的中点,过点C作CE⊥BD,垂足为E. 求证:BE= DE+AD.
【问题探究】小明同学的思路是:如图2,在BE上截取BF= AD,连接CA,CB,CD,CF……
请你按照小明的思路将上述问题的证明过程补充完整.
证明过程补充如下:因为C为$\overset{\frown}{AB}$的中点,所以$\overset{\frown}{AC}=\overset{\frown}{BC}$,所以AC=BC.在△ADC和△BFC中,因为$\left\{\begin{array}{l}AD=BF,\\ \angle DAC=\angle FBC,\\ AC=BC,\end{array}\right.$所以△ADC≌△BFC,所以CD=CF.因为CE⊥BD,所以DE=EF.因为BE=EF+BF,所以BE=DE+AD.
【结论运用】如图3,△ABC是⊙O的内接等边三角形,D是$\widehat{AB}$上一点,连接BD,CD,∠ACD= 45°,过点A作AE⊥CD,垂足为E. 若AB= $4\sqrt{2}$,则△BCD的周长为______.
$4\sqrt{2}+8$
【变式探究】如图4,若将【问题发现】中“C为$\widehat{AB}$的中点”改为“C为优弧AB的中点”,其他条件不变,上述结论“BE= DE+AD”还成立吗?若成立,请说明理由;若不成立,请写出BE,AD,DE之间的新等量关系,并加以证明.
BE=DE+AD不成立,新等量关系为DE=BE+AD.证明如下:在DE上截取DF=AD,连接AC,DC,FC,BC.因为C为优弧AB的中点,所以$\overset{\frown}{AC}=\overset{\frown}{BC}$,所以AC=BC,∠ADC=∠BDC.在△ADC和△FDC中,因为$\left\{\begin{array}{l}AD=FD,\\ \angle ADC=\angle FDC,\\ DC=DC,\end{array}\right.$所以△ADC≌△FDC,所以AC=FC.因为AC=BC,所以FC=BC.因为CE⊥BD,所以BE=EF.因为DE=EF+DF,所以DE=BE+AD.
答案:
解:[问题探究]证明过程补充如下:因为C为$\overset{\frown}{AB}$的中点,所以$\overset{\frown}{AC}=\overset{\frown}{BC}$,所以AC=BC.在△ADC和△BFC中,因为$\left\{\begin{array}{l}AD=BF,\\ \angle DAC=\angle FBC,\\ AC=BC,\end{array}\right.$所以△ADC≌△BFC,所以CD=CF.因为CE⊥BD,所以DE=EF.因为BE=EF+BF,所以BE=DE+AD. [结论运用]$4\sqrt{2}+8$ 提示:因为AE⊥CD,所以∠AEC=90°.又因为∠ACD=45°,所以∠EAC=45°,所以∠ACE=∠EAC,所以AE=CE.因为△ABC为等边三角形,所以BC=AC=AB=$4\sqrt{2}$.因为AE²+CE²=AC²,所以2CE²=$(4\sqrt{2})^{2}$,解得CE=4.由[问题探究]可知,CE=DE+BD=4,所以△BCD的周长为BC+BD+CD=BC+BD+CE+DE=BC+2(DE+BD)=$4\sqrt{2}+8$. [变式探究]BE=DE+AD不成立,新等量关系为DE=BE+AD.证明如下:在DE上截取DF=AD,连接AC,DC,FC,BC.因为C为优弧AB的中点,所以$\overset{\frown}{AC}=\overset{\frown}{BC}$,所以AC=BC,∠ADC=∠BDC.在△ADC和△FDC中,因为$\left\{\begin{array}{l}AD=FD,\\ \angle ADC=\angle FDC,\\ DC=DC,\end{array}\right.$所以△ADC≌△FDC,所以AC=FC.因为AC=BC,所以FC=BC.因为CE⊥BD,所以BE=EF.因为DE=EF+DF,所以DE=BE+AD.
查看更多完整答案,请扫码查看


