《2025年小题狂做九年级数学上册苏科版提优版》

1. 如图,$AB是\odot O$的直径,半径$OC\perp AB$. 若点$D在劣弧CB上由点C向点B$运动(不与点$B,C$重合),且$DE\perp OC,DF\perp AB$,垂足分别是$E,F$,则$EF$的长度 (C)

A.逐渐变大
B.逐渐变小
C.不变
D.先变小后变大

答案： C

2. 如图,点$A,B,C在\odot O$上,四边形$ABCO$是平行四边形. 若$OA= 2$,则四边形$ABCO$的面积为2√3.

答案： 2√3

3. 把一张圆形纸片按如图所示的方式折叠两次后展开,图中的虚线表示折痕,连接$OB,OC$,则$\angle BOC$(小于$180^{\circ }$)的度数为______150°.

答案： 150°

4. (2024 盐城市盐都区期中)如图,在矩形$ABCD$中,$AB= 12,BC= 16$,$E,F分别是边AB,BC$上的动点,且$EF= 10$,$G是EF$的中点,连接$AG,CG$,则四边形$AGCD$面积的最小值为142.

答案： 142 提示:如图,连接 AC,BG,过点 B 作 BH⊥AC 于点 H.因为四边形 ABCD 是矩形,所以∠EBF=90°.因为 EF=10,G 是 EF 的中点,所以BG=1/2EF=1/2×10=5,所以点 G 在以点 B 为圆心,5 为半径的1/4圆弧上.设该弧与 BH 交于点 G',过点 G 作 GH'⊥AC,易证 GH'≥G'H.又因为S△ACG=1/2AC·GH',所以当点 G 运动到点 G'处时,S△ACG 最小,此时四边形 AGCD 的面积最小,最小值即为四边形 AG'CD 的面积.因为 AB=12=CD,BC=16=AD,所以 AC=√(AB²+BC²)=20,S△ACD=1/2AD·CD=96.由等积法,得 BH=AB·BC/AC=48/5,所以 G'H=BH-BG'=48/5-5=23/5,所以 S△ACG'=1/2AC·G'H=1/2×20×23/5=46,所以 S四边形AG'CD=S△ACD+S△ACG'=96+46=142,即四边形 AGCD 面积的最小值是 142.

5. 如图,$AB和OC分别是\odot O$的直径和半径,$\angle BOC= 60^{\circ }$,$P是直径AB$上的一个动点,射线$CP与\odot O相交于点Q$,连接$OQ$. 若$\triangle POQ$是等腰三角形,则$\angle CPB$的度数为______40°或 80°或 100°.

答案： 40°或 80°或 100° 提示:①当 OP=PQ 且点 P 在 OB 上时,如图 1,由条件可设∠OCQ=∠OQC=∠POQ=α,因为∠BOC=60°,所以 3α+60°=180°,解得 α=40°,所以∠CPB=α+60°=100°;当 OP=PQ 且点 P 在 OA 上时,如图 2,由条件可设∠OCQ=∠OQC=∠POQ=α,因为∠BOC=60°,所以∠AOC=180°-∠BOC=120°,所以 3α+120°=180°,解得 α=20°,所以∠CPB=∠POQ+∠OQP=2α=40°.②当 OQ=PQ 时,如图 3.因为 OC=OQ,所以可设∠OCQ=∠OQC=α.因为 OQ=PQ,所以可设∠QOP=∠OPQ=β.因为∠BOC=60°,所以根据三角形内角和定理可得{α+2β=180°,2α+β+60°=180°,解得{α=20°,β=80°.所以∠CPB=∠OPQ=β=80°.③当 OP=OQ 时,点 P 在⊙O 上,即点 P 与点 A 或点 B 重合,所以此时点 P 与点 Q 重合,三角形不存在.综上所述,∠CPB 的度数为 40°或 80°或 100°.

6. 如图,直线$y= \frac {3}{4}x+3与坐标轴交于A,B$两点,已知$\odot O$的半径为2. 若$P是\odot O$上的一个动点,则$\triangle ABP$的面积的最大值为11.

答案： 11 提示:根据题意,易知点 A(-4,0),B(0,3),所以 OA=4,OB=3.在 Rt△AOB 中,根据勾股定理,得 AB=√(OA²+OB²)=5.因为在△ABP 中,AB 的长是定值,所以要使△ABP 的面积最大,则 P 为⊙O 上到 AB 的距离最大的一点.过点 O 作 OC⊥AB 于点 C,延长 CO 交⊙O 于点 P,此时△ABP 的面积最大.因为 S△AOB=1/2OA·OB=1/2AB·OC,所以 OC=12/5.因为⊙O 的半径为 2,所以 CP=OC+OP=22/5.所以△ABP 的面积的最大值为 1/2AB·CP=1/2×5×22/5=11.

7. $A是\odot O$外一点,直线$AO交\odot O于C,D$两点,$E是\odot O$上的一点(不与点$C,D$重合),直线$AE交\odot O于另一点B$,$AB= OC$.
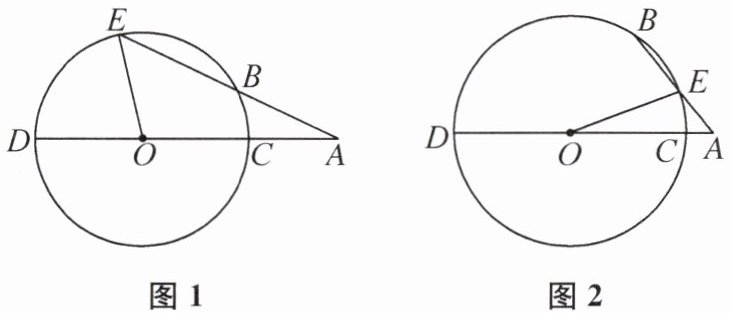
(1)如图1,当点$B在线段AE$上时,求$\angle DOE与\angle A$之间的关系.
(2)如图2,当点$E在线段AB$上时,请判断(1)中的结论是否成立,并说明理由.

答案： 解:
(1)连接 OB,则 OB=OC.因为 AB=OC,所以 OB=AB,所以∠AOB=∠A.因为 OE=OB,所以∠OBE=∠E.因为∠OBE=∠AOB+∠A=2∠A,所以∠E=2∠A,所以∠DOE=∠E+∠A=3∠A.（2）成立,理由如下:连接 OB,则 OB=OC.因为 AB=OC,所以 OB=AB,所以∠AOB=∠A,所以∠B=180°-2∠A.因为 OB=OE,所以∠B=∠OEB,所以∠BOE=180°-2∠B=180°-2(180°-2∠A)=4∠A-180°,所以∠DOE=∠BOD+∠BOE=180°-∠AOB+∠BOE=180°-∠A+4∠A-180°=3∠A.