第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1.(2024 盐城市盐都区期中)国庆期间,某热门题材电影凭借优秀的制作,一上映就获得全国人民的追捧. 据统计,该电影在某地第一天票房约 3 亿元,若以后每天票房按相同的增长率增长,三天后票房收入累计达 18 亿元. 若把增长率记作 x,则方程可以列为 (
A.$3(1+x)= 18$
B.$3(1+x)^{2}= 18$
C.$3+3(1+x)^{2}= 18$
D.$3+3(1+x)+3(1+x)^{2}= 18$
D
)A.$3(1+x)= 18$
B.$3(1+x)^{2}= 18$
C.$3+3(1+x)^{2}= 18$
D.$3+3(1+x)+3(1+x)^{2}= 18$
答案:
D
2. 某市体育局要组织一次篮球赛,赛制为单循环形式(每两队之间都只赛一场),计划安排 28 场比赛,则应邀请
8
支球队参赛.
答案:
8
3.(2024 重庆市中考)随着经济复苏,某公司近两年的总收入逐年递增. 该公司 2021 年缴税 40 万元,2023 年缴税 48.4 万元. 该公司这两年缴税的年平均增长率是______
10%
.
答案:
10%
4. 某小型工厂 9 月份生产的 A,B 两种产品数量分别为 200 件和 100 件,A,B 两种产品出厂单价之比为 $2:1$. 由于订单的增加,工厂提高了 A,B 两种产品的生产数量和出厂单价,10 月份 A 产品生产数量的增长率和 A 产品出厂单价的增长率相等,B 产品生产数量的增长率是 A 产品生产数量的增长率的一半,B 产品出厂单价的增长率是 A 产品出厂单价的增长率的 2 倍. 设 B 产品生产数量的增长率为 $x(x>0)$.
(1)用含有 x 的代数式填表(不需化简):
|产品|9月份生产数量/件|生产数量的增长率|10月份生产数量/件|
|A|200|
|B|100|x|

(2)若 9 月份两种产品出厂单价的和为 90 元,10 月份该工厂总收入的增长率为 4.4x,求 x 的值(用百分数表示).
(1)用含有 x 的代数式填表(不需化简):
|产品|9月份生产数量/件|生产数量的增长率|10月份生产数量/件|
|A|200|
2x
|200(1+2x)
||B|100|x|
100(1+x)
|
(2)若 9 月份两种产品出厂单价的和为 90 元,10 月份该工厂总收入的增长率为 4.4x,求 x 的值(用百分数表示).
解:由题意可知,9月份A产品的出厂单价为90×$\frac{2}{2+1}$=60(元),B产品的出厂单价为90−60=30(元).根据题意,得60(1+2x)×200(1+2x)+30(1+4x)×100(1+x)=(60×200+30×100)(1+4.4x).整理,得20x²−x=0,解得x₁=0(舍去),x₂=0.05=5%.答:x的值为5%.
答案:
解:
(1)2x 200(1+2x) 100(1+x)
(2)由题意可知,9月份A产品的出厂单价为90×$\frac{2}{2+1}$=60(元),B产品的出厂单价为90−60=30(元).根据题意,得60(1+2x)×200(1+2x)+30(1+4x)×100(1+x)=(60×200+30×100)(1+4.4x).整理,得20x²−x=0,解得x₁=0(舍去),x₂=0.05=5%.答:x的值为5%.
(1)2x 200(1+2x) 100(1+x)
(2)由题意可知,9月份A产品的出厂单价为90×$\frac{2}{2+1}$=60(元),B产品的出厂单价为90−60=30(元).根据题意,得60(1+2x)×200(1+2x)+30(1+4x)×100(1+x)=(60×200+30×100)(1+4.4x).整理,得20x²−x=0,解得x₁=0(舍去),x₂=0.05=5%.答:x的值为5%.
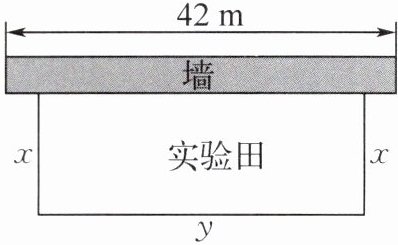
5.(2024 无锡市宜兴市期中)如图,某校劳动实践基地用总长为 80 m 的栅栏,围成一块一边靠墙的矩形实验田,已知墙长为 42 m,栅栏在安装过程中不重叠、无损耗. 设矩形实验田与墙垂直的一边长为 x m,与墙平行的一边长为 y m,面积为 $S\ \text{m}^2$.
(1)直接写出 y 与 x,S 与 x 之间的函数表达式(不要求写 x 的取值范围).
(2)矩形实验田的面积 S 能达到 $750\ \text{m}^2$ 吗?如果能,求出 x 的值;如果不能,请说明理由.
(3)矩形实验田的面积 S 能达到 $850\ \text{m}^2$ 吗?如果能,求出 x 的值;如果不能,请说明理由. 你能求出矩形实验田的面积 S 的最大值吗?若能,请求出 S 的最大值并求出此时 x 的值.
]
(1)直接写出 y 与 x,S 与 x 之间的函数表达式(不要求写 x 的取值范围).
(2)矩形实验田的面积 S 能达到 $750\ \text{m}^2$ 吗?如果能,求出 x 的值;如果不能,请说明理由.
(3)矩形实验田的面积 S 能达到 $850\ \text{m}^2$ 吗?如果能,求出 x 的值;如果不能,请说明理由. 你能求出矩形实验田的面积 S 的最大值吗?若能,请求出 S 的最大值并求出此时 x 的值.
]

答案:
解:
(1)y=-2x+80,S=x(-2x+80)=-2x²+80x.
(2)矩形实验田的面积S能达到750 m².当S=750时,-2x²+80x=750,x²-40x+375=0,解得x=25或x=15,此时y=30或y=50.因为30<42,所以当x=25 m时,矩形实验田的面积S能达到750 m².
(3)矩形实验田的面积S不能达到850 m².理由如下:当S=850时,-2x²+80x=850,x²-40x+425=0.因为根的判别式(-40)²-4×425=-100<0,所以方程-2x²+80x=850没有实数根,所以矩形实验田的面积S不能达到850 m².因为S=-2x²+80x=-2(x²-40x)=-2(x²-40x+400-400)=-2(x-20)²+800≤800,所以当x=20时,S有最大值,此时y=40<42,符合题意,所以S的最大值为800 m²,此时x的值为20.
(1)y=-2x+80,S=x(-2x+80)=-2x²+80x.
(2)矩形实验田的面积S能达到750 m².当S=750时,-2x²+80x=750,x²-40x+375=0,解得x=25或x=15,此时y=30或y=50.因为30<42,所以当x=25 m时,矩形实验田的面积S能达到750 m².
(3)矩形实验田的面积S不能达到850 m².理由如下:当S=850时,-2x²+80x=850,x²-40x+425=0.因为根的判别式(-40)²-4×425=-100<0,所以方程-2x²+80x=850没有实数根,所以矩形实验田的面积S不能达到850 m².因为S=-2x²+80x=-2(x²-40x)=-2(x²-40x+400-400)=-2(x-20)²+800≤800,所以当x=20时,S有最大值,此时y=40<42,符合题意,所以S的最大值为800 m²,此时x的值为20.
查看更多完整答案,请扫码查看


