第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图,冰淇淋蛋筒下部呈圆锥形,则蛋筒圆锥部分包装纸的面积(接缝忽略不计)为(
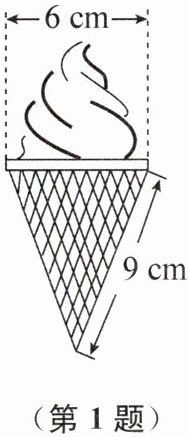
$A. 27 cm^2$
$B. 54 cm^2$
$C. 27π cm^2$
$D. 54π cm^2$
C
)
$A. 27 cm^2$
$B. 54 cm^2$
$C. 27π cm^2$
$D. 54π cm^2$
答案:
C
2. 如图,圆锥形冰淇淋盒的母线长是 13 cm,高是 12 cm,则该圆锥的底面圆的面积是(
$A. 10π cm^2$
$B. 25π cm^2$
$C. 60π cm^2$
$D. 65π cm^2$
B
)$A. 10π cm^2$
$B. 25π cm^2$
$C. 60π cm^2$
$D. 65π cm^2$
答案:
B
3. (2024 扬州市中考)若用半径为 10 cm 的半圆形纸片围成一个圆锥的侧面,则这个圆锥底面圆的半径为
5
cm.
答案:
5
4. 如图,在△ABC 中,AC= 3,AB= 4,边 BC 上的高 AD= 2,将△ABC 绕着 BC 所在的直线旋转一周得到的几何体的表面积为______
14π
.
答案:
14π
5. (2024 徐州市中考)将圆锥的侧面沿一条母线剪开后展平,所得扇形的面积为$ 4π cm^2,$圆心角θ为 90°,圆锥的底面圆的半径为______
1
cm.
答案:
1
6. (2024 广东省中考)综合与实践.
【主题】滤纸与漏斗.
【素材】如图1所示:
①一张直径为 10 cm 的圆形滤纸;
②一只漏斗口直径与母线均为 7 cm 的圆锥形过滤漏斗.
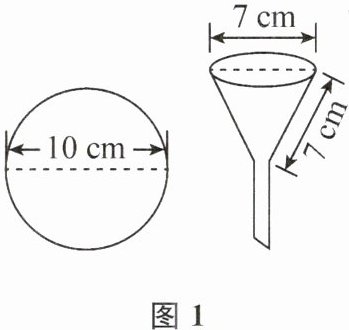
【实践操作】
步骤 1:取一张滤纸;
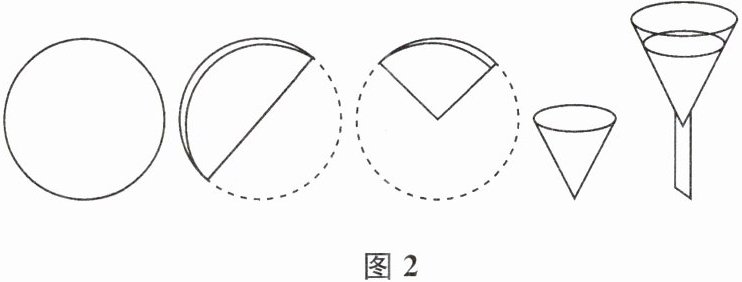
步骤 2:按如图2所示步骤折叠好滤纸;
步骤 3:将其中一层撑开,围成圆锥形;
步骤 4:将围成圆锥形的滤纸放入如图1所示漏斗中.
【实践探索】
(1)滤纸是否能紧贴此漏斗内壁(忽略漏斗管口处)?用你所学的数学知识说明.
(2)当滤纸紧贴漏斗内壁时,求滤纸围成圆锥形的体积(结果保留π).
【主题】滤纸与漏斗.
【素材】如图1所示:
①一张直径为 10 cm 的圆形滤纸;
②一只漏斗口直径与母线均为 7 cm 的圆锥形过滤漏斗.


【实践操作】
步骤 1:取一张滤纸;
步骤 2:按如图2所示步骤折叠好滤纸;
步骤 3:将其中一层撑开,围成圆锥形;
步骤 4:将围成圆锥形的滤纸放入如图1所示漏斗中.
【实践探索】
(1)滤纸是否能紧贴此漏斗内壁(忽略漏斗管口处)?用你所学的数学知识说明.
(2)当滤纸紧贴漏斗内壁时,求滤纸围成圆锥形的体积(结果保留π).
答案:
解:
(1) 滤纸能紧贴此漏斗内壁,理由如下:设圆锥底面圆半径为r,母线长为R. 由2πr=$\frac{nπR}{180}$,得$\frac{n}{360}$=$\frac{r}{R}$. 图1中,滤纸围成的圆锥圆心角$n_1$=90°×2=180°;图2中,当滤纸能紧贴时,$\frac{r}{R}$=$\frac{3.5}{7}$=$\frac{1}{2}$,所以$n_2$=180°. 因为$n_1$=$n_2$,所以滤纸能紧贴此漏斗内壁.
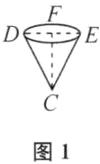
(2) 如图1,由
(1)知,CD=DE=CE=5cm,所以∠CDE=60°. 过点C作CF⊥DE于点F,则DF=$\frac{1}{2}$DE=$\frac{5}{2}$cm. 在Rt△CDF中,由勾股定理,得CF=$\sqrt{CD^{2}-DF^{2}}$=$\frac{5\sqrt{3}}{2}$cm,所以圆锥体的体积V=π×$(\frac{5}{2})^{2}$×$\frac{5\sqrt{3}}{2}$×$\frac{1}{3}$=$\frac{125\sqrt{3}}{24}$π($cm^{3}$).答:圆锥形的体积是$\frac{125\sqrt{3}}{24}$π$cm^{3}$.
解:
(1) 滤纸能紧贴此漏斗内壁,理由如下:设圆锥底面圆半径为r,母线长为R. 由2πr=$\frac{nπR}{180}$,得$\frac{n}{360}$=$\frac{r}{R}$. 图1中,滤纸围成的圆锥圆心角$n_1$=90°×2=180°;图2中,当滤纸能紧贴时,$\frac{r}{R}$=$\frac{3.5}{7}$=$\frac{1}{2}$,所以$n_2$=180°. 因为$n_1$=$n_2$,所以滤纸能紧贴此漏斗内壁.


(2) 如图1,由
(1)知,CD=DE=CE=5cm,所以∠CDE=60°. 过点C作CF⊥DE于点F,则DF=$\frac{1}{2}$DE=$\frac{5}{2}$cm. 在Rt△CDF中,由勾股定理,得CF=$\sqrt{CD^{2}-DF^{2}}$=$\frac{5\sqrt{3}}{2}$cm,所以圆锥体的体积V=π×$(\frac{5}{2})^{2}$×$\frac{5\sqrt{3}}{2}$×$\frac{1}{3}$=$\frac{125\sqrt{3}}{24}$π($cm^{3}$).答:圆锥形的体积是$\frac{125\sqrt{3}}{24}$π$cm^{3}$.
查看更多完整答案,请扫码查看


