第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 已知$\odot O$的弦 AB 等于半径的$\sqrt {2}$倍,那么弦 AB 所对的圆周角是(
A.$45^{\circ }$
B.$135^{\circ }$
C.$45^{\circ }或135^{\circ }$
D.$90^{\circ }$
C
)A.$45^{\circ }$
B.$135^{\circ }$
C.$45^{\circ }或135^{\circ }$
D.$90^{\circ }$
答案:
C
2. (2024 南京市雨花台区期中)如图,在$\odot O$的内接四边形 ABCD 中,若$\odot O$的半径为1,$AB= 1,CD= \sqrt {2}$,则$∠C+∠D$的度数为(
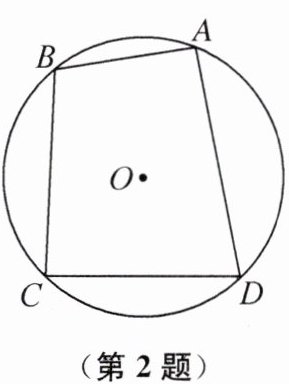
A.$120^{\circ }$
B.$135^{\circ }$
C.$150^{\circ }$
D.$165^{\circ }$
D
)
A.$120^{\circ }$
B.$135^{\circ }$
C.$150^{\circ }$
D.$165^{\circ }$
答案:
D
3. (2024 武汉市中考)如图,四边形 ABCD 内接于$\odot O$,$∠ABC= 60^{\circ },∠BAC= ∠CAD= 45^{\circ },AB+AD= 2$,则$\odot O$的半径是(
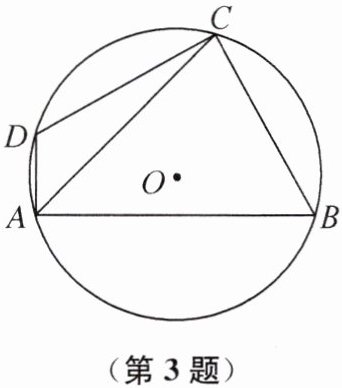
A.$\frac {\sqrt {6}}{3}$
B.$\frac {2\sqrt {2}}{3}$
C.$\frac {\sqrt {3}}{2}$
D.$\frac {\sqrt {2}}{2}$
A
)
A.$\frac {\sqrt {6}}{3}$
B.$\frac {2\sqrt {2}}{3}$
C.$\frac {\sqrt {3}}{2}$
D.$\frac {\sqrt {2}}{2}$
答案:
A 提示:如图,延长AB至点E,使$BE = AD$,连接BD,CE. 因为$AB + AD = 2$,所以$AB + BE = AE = 2$.因为四边形ABCD内接于$\odot O$,所以$∠ADC + ∠ABC = 180^{\circ}$. 又因为$∠ABC + ∠CBE = 180^{\circ}$,所以$∠ADC = ∠CBE$. 因为$∠BAC = ∠CAD = 45^{\circ}$,所以$∠CDB = ∠CBD = 45^{\circ}$,所以$DC = BC$,$∠DCB = 90^{\circ}$,所以$\triangle ADC\cong \triangle EBC(SAS)$,所以$∠ACD = ∠ECB$,$CA = CE$,所以$∠ACE = ∠DCB = 90^{\circ}$,所以$\triangle ACE$是等腰直角三角形,所以$AC = \frac{\sqrt{2}}{2}AE = \sqrt{2}$,连接CO并延长交$\odot O$于点F,连接AF,则$∠FAC = 90^{\circ}$. 又因为$∠AFC = ∠ABC = 60^{\circ}$,所以$∠ACF = 30^{\circ}$. 设$\odot O$的半径为r. 在$Rt\triangle ACF$中,由勾股定理,得$AC^{2} + AF^{2} = CF^{2}$,即$r^{2} + (\sqrt{2})^{2} = (2r)^{2}$,解得$r = \frac{\sqrt{6}}{3}$(负值已舍).
4. 如图,四边形 ABCD 是半圆 O 的内接四边形,AB 是直径,$\widehat {DC}= \widehat {CB}$.若$∠BCD= 110^{\circ }$,则$∠ABC$的度数为______
$55^{\circ}$
.
答案:
$55^{\circ}$
5. 如图,四边形 ABCD 内接于$\odot O$,它的 3 个外角$∠EAB,∠FBC,∠GCD的度数之比为1:2:4$,则$∠D= $
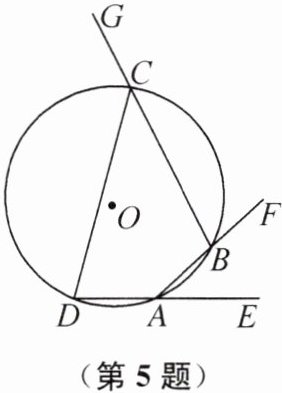
72
°.
答案:
72 提示:由题意可设,$∠EAB = x$,$∠FBC = 2x$,$∠GCD = 4x$,所以$∠BAD = 180^{\circ} - x$,$∠BCD = 180^{\circ} - 4x$. 因为四边形ABCD为圆内接四边形,所以$∠BAD + ∠BCD = 180^{\circ}$,$∠D + ∠ABC = 180^{\circ}$,所以$180^{\circ} - x + 180^{\circ} - 4x = 180^{\circ}$,解得$x = 36^{\circ}$,所以$∠FBC = 2x = 72^{\circ}$. 因为$∠FBC + ∠ABC = 180^{\circ}$,所以$∠D = ∠FBC = 72^{\circ}$.
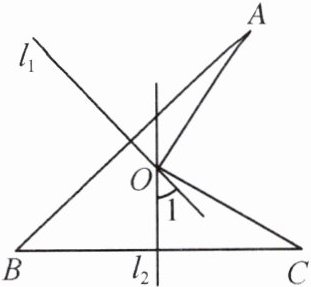
6. 如图,线段 AB,BC 的垂直平分线$l_{1},l_{2}$相交于点 O.若$∠1= 39^{\circ }$,则$∠AOC= $______.
]
]

$78^{\circ}$
答案:
$78^{\circ}$ 提示:记直线$l_{1},l_{2}$与AB,BC的垂足分别为E,F,则由条件可知,O,E,B,F四点共圆,所以由圆内接四边形对角互补的性质可知,$∠ABC + ∠EOF = 180^{\circ}$. 因为$∠1 + ∠EOF = 180^{\circ}$,所以$∠ABC = ∠1 = 39^{\circ}$. 连接OB,AC. 由垂直平分线的性质可知,$OB = OA = OC$. 所以O是$\triangle ABC$的外心,所以$∠AOC = 2∠ABC = 78^{\circ}$.
7. (2024 扬州市中考)如图,在$\triangle ABC$中,$CA= CB$,$\odot O是\triangle ABC$的外接圆,点 D 在$\odot O上(AD>BD)$,连接 AD,BD,CD.
【特殊化感知】
(1)如图 1,若$∠ACB= 60^{\circ }$,点 D 在 AO 延长线上,则 AD-BD 与 CD 的数量关系为______
【一般化探究】
(2)如图 2,若$∠ACB= 60^{\circ }$,点 C,D 在 AB 同侧,判断 AD-BD 与 CD 的数量关系并说明理由.
]
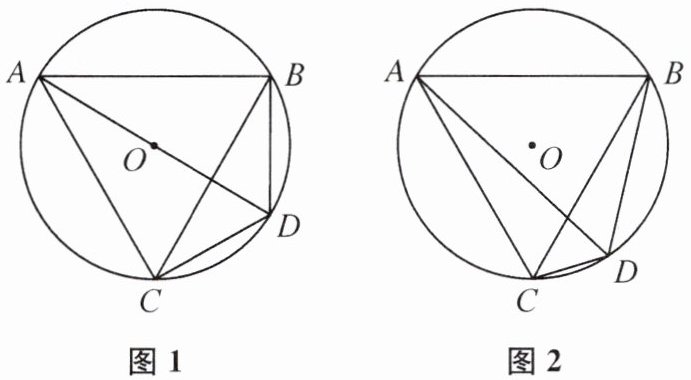
$AD - BD = CD$. 理由如下:
如图,延长BD至点E使$DE = CD$,连接CE. 因为$CA = CB$,$∠ACB = 60^{\circ}$,所以$\triangle ABC$为等边三角形,所以$∠BAC = ∠ABC = 60^{\circ}$,所以$∠CDE = 180^{\circ} - ∠BDC = ∠BAC = 60^{\circ}$. 因为$DE = CD$,所以$\triangle CDE$为等边三角形,所以$CE = CD$,$∠DCE = ∠E = 60^{\circ}$,所以$∠ACD = ∠ACB + ∠BCD = 60^{\circ} + ∠BCD = ∠BCE$. 因为$∠ADC = ∠ABC = 60^{\circ}$,所以$∠ADC = ∠E = 60^{\circ}$. 在$\triangle ACD$和$\triangle BCE$中,$\begin{cases} ∠ACD = ∠BCE \\ CD = CE \\ ∠ADC = ∠E \end{cases}$,所以$\triangle ACD\cong \triangle BCE$,所以$AD = BE$,因为$BE = BD + DE = BD + CD$,所以$AD = BD + CD$,所以$AD - BD = CD$.
【特殊化感知】
(1)如图 1,若$∠ACB= 60^{\circ }$,点 D 在 AO 延长线上,则 AD-BD 与 CD 的数量关系为______
$AD - BD = CD$
;【一般化探究】
(2)如图 2,若$∠ACB= 60^{\circ }$,点 C,D 在 AB 同侧,判断 AD-BD 与 CD 的数量关系并说明理由.
]

$AD - BD = CD$. 理由如下:
如图,延长BD至点E使$DE = CD$,连接CE. 因为$CA = CB$,$∠ACB = 60^{\circ}$,所以$\triangle ABC$为等边三角形,所以$∠BAC = ∠ABC = 60^{\circ}$,所以$∠CDE = 180^{\circ} - ∠BDC = ∠BAC = 60^{\circ}$. 因为$DE = CD$,所以$\triangle CDE$为等边三角形,所以$CE = CD$,$∠DCE = ∠E = 60^{\circ}$,所以$∠ACD = ∠ACB + ∠BCD = 60^{\circ} + ∠BCD = ∠BCE$. 因为$∠ADC = ∠ABC = 60^{\circ}$,所以$∠ADC = ∠E = 60^{\circ}$. 在$\triangle ACD$和$\triangle BCE$中,$\begin{cases} ∠ACD = ∠BCE \\ CD = CE \\ ∠ADC = ∠E \end{cases}$,所以$\triangle ACD\cong \triangle BCE$,所以$AD = BE$,因为$BE = BD + DE = BD + CD$,所以$AD = BD + CD$,所以$AD - BD = CD$.
答案:
(1)$AD - BD = CD$ 提示:因为$CA = CB$,$∠ACB = 60^{\circ}$,所以$\triangle ABC$为等边三角形,所以$∠BAC = 60^{\circ}$. 因为AD为$\odot O$的直径,所以$∠ABD = ∠ACD = 90^{\circ}$,$∠BAD = ∠CAD = \frac{1}{2}∠BAC = 30^{\circ}$,所以$CD = BD = \frac{1}{2}AD$,所以$AD - BD = CD$.
(2)$AD - BD$与CD的数量关系为$AD - BD = CD$. 理由如下:
如图,延长BD至点E使$DE = CD$,连接CE. 因为$CA = CB$,$∠ACB = 60^{\circ}$,所以$\triangle ABC$为等边三角形,所以$∠BAC = ∠ABC = 60^{\circ}$,所以$∠CDE = 180^{\circ} - ∠BDC = ∠BAC = 60^{\circ}$. 因为$DE = CD$,所以$\triangle CDE$为等边三角形,所以$CE = CD$,$∠DCE = ∠E = 60^{\circ}$,所以$∠ACD = ∠ACB + ∠BCD = 60^{\circ} + ∠BCD = ∠BCE$. 因为$∠ADC = ∠ABC = 60^{\circ}$,所以$∠ADC = ∠E = 60^{\circ}$. 在$\triangle ACD$和$\triangle BCE$中,$\begin{cases} ∠ACD = ∠BCE \\ CD = CE \\ ∠ADC = ∠E \end{cases}$,所以$\triangle ACD\cong \triangle BCE$,所以$AD = BE$,因为$BE = BD + DE = BD + CD$,所以$AD = BD + CD$,所以$AD - BD = CD$.
(1)$AD - BD = CD$ 提示:因为$CA = CB$,$∠ACB = 60^{\circ}$,所以$\triangle ABC$为等边三角形,所以$∠BAC = 60^{\circ}$. 因为AD为$\odot O$的直径,所以$∠ABD = ∠ACD = 90^{\circ}$,$∠BAD = ∠CAD = \frac{1}{2}∠BAC = 30^{\circ}$,所以$CD = BD = \frac{1}{2}AD$,所以$AD - BD = CD$.
(2)$AD - BD$与CD的数量关系为$AD - BD = CD$. 理由如下:
如图,延长BD至点E使$DE = CD$,连接CE. 因为$CA = CB$,$∠ACB = 60^{\circ}$,所以$\triangle ABC$为等边三角形,所以$∠BAC = ∠ABC = 60^{\circ}$,所以$∠CDE = 180^{\circ} - ∠BDC = ∠BAC = 60^{\circ}$. 因为$DE = CD$,所以$\triangle CDE$为等边三角形,所以$CE = CD$,$∠DCE = ∠E = 60^{\circ}$,所以$∠ACD = ∠ACB + ∠BCD = 60^{\circ} + ∠BCD = ∠BCE$. 因为$∠ADC = ∠ABC = 60^{\circ}$,所以$∠ADC = ∠E = 60^{\circ}$. 在$\triangle ACD$和$\triangle BCE$中,$\begin{cases} ∠ACD = ∠BCE \\ CD = CE \\ ∠ADC = ∠E \end{cases}$,所以$\triangle ACD\cong \triangle BCE$,所以$AD = BE$,因为$BE = BD + DE = BD + CD$,所以$AD = BD + CD$,所以$AD - BD = CD$.
查看更多完整答案,请扫码查看


