《2025年小题狂做九年级数学上册苏科版提优版》

1. 某跳远队准备从甲、乙、丙、丁4名运动员中选取1名成绩优异且发挥稳定的运动员参加比赛,他们成绩的平均数和方差如下：$\overline {x}_{甲}= \overline {x}_{丁}= 5.75$,$\overline {x}_{乙}= \overline {x}_{丙}= 6.15$,$s^{2}_{甲}= s^{2}_{丙}= 0.02$,$s^{2}_{乙}= s^{2}_{丁}= 0.45$,则应选择的运动员是(C)
A.甲
B.乙
C.丙
D.丁

答案： C

2. 已知一组数据3,a,4,6,7的平均数是5,那么这组数据的方差是(B)
A.$\sqrt {2}$
B.2
C.$\sqrt {10}$
D.10

答案： B

3. 某排球队6名场上队员的身高(单位：cm)是：180,184,188,190,192,194. 现用一名身高为188 cm的队员换下场上身高为194 cm的队员,与换人前相比,场上队员的身高(A)
A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变小
D.平均数变大,方差变大

答案： A

4. 八年级(1)班的学生升九年级时,下列有关年龄的统计量不变的是(B)
A.平均年龄
B.年龄的方差
C.年龄的众数
D.年龄的中位数

答案： B

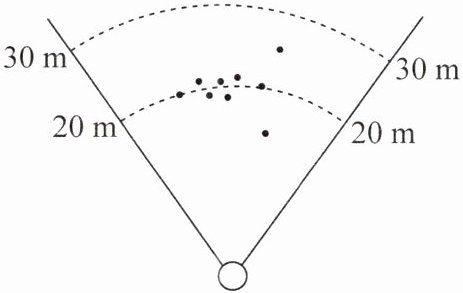
5. (2024常州市中考)小丽进行投掷标枪训练,总共投掷10次,前9次标枪的落点如图所示,记录成绩(单位：m),此时这组成绩的平均数是20 m,方差是$s^{2}_{1}m^{2}$. 若第10次投掷标枪的落点恰好在20 m线上,且投掷结束后这组成绩的方差是$s^{2}_{2}m^{2}$,则$s^{2}_{1}$＞$s^{2}_{2}$(填“＞”“＜”或“=”).

答案： ＞ 提示:由题意可得,前9次标枪的平均数和10次投掷标枪的平均数相同,均为20 m.因为第10次投掷标枪的落点恰好在20 m线上,所以$s_{2}^{2}=\frac{9}{10}s_{1}^{2}$,所以$s_{1}^{2}＞s_{2}^{2}$.

6. 若一组数据的方差$s^{2}= \frac {1}{5}[(6-10)^{2}+(9-10)^{2}+(a-10)^{2}+(11-10)^{2}+(b-10)^{2}]= 6.8$,则$a^{2}+b^{2}$的值为______296.

答案： 296 提示:将题中等式化简,得$a^{2}+b^{2}-20(a+b)+184=0$①.又由条件易知,原数据为6,9,a,11,b,且平均数为10,所以6+9+a+11+b=10×5,所以a+b=24②.将②代入①,解得$a^{2}+b^{2}=296$.

(1)根据以上数据把表格补充完整：
18 18 15 11
(2)请你帮助张老师选择其中一种上班路线,并利用以上至少2个统计量说明理由.
因为路线二的平均数小于路线一,路线二的中位数小于路线一,所以选路线二。

答案：
(1) 18 18 15 11 提示:路线一:15,16,17,18,18,18,19,19,20,20.平均数为$\frac{15+16+17+18×3+19×2+20×2}{10}=18$,众数为18.路线二:11,11,11,12,14,16,17,21,21,22.中位数为$\frac{14+16}{2}=15$,极差为22-11=11.
(2) 因为路线二的平均数小于路线一,路线二的中位数小于路线一,路线二的众数小于路线一,所以选路线二.