第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图,两个同心圆,大圆的半径为5,小圆的半径为3. 若大圆的弦$AB$与小圆有公共点,则弦$AB$的取值范围是 (
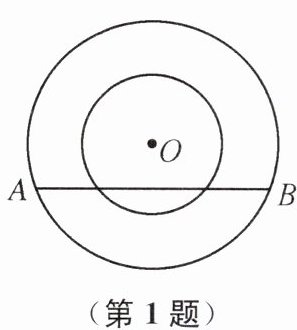
A.$8\leq AB\leq 10$
B.$8< AB\leq 10$
C.$4\leq AB\leq 5$
D.$4< AB\leq 5$
A
)
A.$8\leq AB\leq 10$
B.$8< AB\leq 10$
C.$4\leq AB\leq 5$
D.$4< AB\leq 5$
答案:
A
2. 如图,直线$y= \frac{\sqrt{3}}{3}x+\sqrt{3}与x$轴、$y轴分别交于A$,$B$两点,圆心$P的坐标为(1,0)$,$\odot P与y轴相切于点O$. 若将$\odot P沿x$轴向左移动,则当$\odot P$与该直线相交时,横坐标为整数的点$P$的个数是 (
A.2
B.3
C.4
D.5
B
)A.2
B.3
C.4
D.5
答案:
B 提示:若⊙P₁与AB相切,如图所示,过点P₁作P₁E⊥AB于点E,则d=r=1.因为直线y=√3/3x + √3与x轴、y轴分别交于A,B两点,所以点A(-3,0),B(0,√3),所以OA=3,OB=√3.在Rt△AOB中,由勾股定理,得AB=2√3,所以AB=2OB,所以∠BAO=30°,所以AP₁=2P₁E=2,所以点P₁(-1,0).同理,在点A的左侧有点P₂(-5,0)使⊙P₂与AB相切.所以当⊙P与直线AB相交时,横坐标为整数的点P的个数是3.
3. 如图,在直角三角形$ABC$中,$\angle C= 90^\circ$,$BC= 3$,$AC= 4$,$D$,$E分别是AC$,$BC$上的一点,且$DE= 3$. 若以$DE为直径的圆与斜边AB相交于点M$,$N$,则$MN$长的最大值为 (
A.$\frac{8}{5}$
B.2
C.$\frac{12}{5}$
D.$\frac{14}{5}$
C
)A.$\frac{8}{5}$
B.2
C.$\frac{12}{5}$
D.$\frac{14}{5}$
答案:
C 提示:如图,过点C作CF⊥AB于点F.取DE的中点O,过点O作OG⊥AB于点G.连接OC,OM.易知OC=OM=1/2DE=3/2.在Rt△ABC中,由勾股定理,得AB=√(AC² + BC²)=5.因为S△ABC=1/2AC·BC=1/2AB·CF,所以CF=12/5.由垂径定理,得MN=2MG.由勾股定理,得MG=√(OM² - OG²).所以当OG长最小时,MN长最大.因为OC+OG≥CF,即OG≥CF - OC,所以当C,O,G三点共线,且点G与点F重合时,OG长取得最小值,此时OG=CF - OC=12/5 - 3/2=9/10,MG=√(OM² - OG²)=6/5,MN=2MG=12/5,即MN长的最大值为12/5.
4. 如图,半径为2的$\odot P的圆心在直线y= 2x-1$上运动,当$\odot P与x$轴相切时,圆心$P$的坐标为
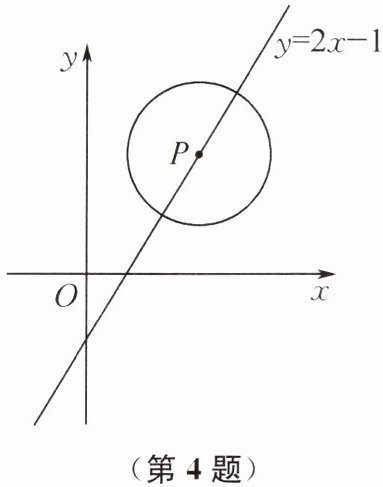
(1.5,2)或(-0.5,-2)
.
答案:
(1.5,2)或(-0.5,-2) 提示:因为⊙P的圆心在直线y=2x - 1上,所以可设点P(x,2x - 1).当⊙P与x轴正半轴相切时,2x - 1=2,解得x=1.5,所以点P(1.5,2);当⊙P与x轴负半轴相切时,2x - 1=-2,解得x=-0.5,所以点P(-0.5,-2).所以点P的坐标为(1.5,2)或(-0.5,-2).
5. 已知$\odot O的半径为R$,点$O到直线l的距离为d$. 若$R$,$d是关于x的方程x^{2}-4x+m= 0$的两个根,则当直线$l与\odot O$相切时,$m$的值为
4
.
答案:
4
6. 如图,在矩形$ABCD$中,$AB= 4$,$BC= 6$,$E为边CD$上的一个动点(不与点$C$,$D$重合),$\odot O是\triangle BCE$的外接圆.
(1)若$CE= 2$,$\odot O交AD于点F$,$G$,求$FG$的长度.
(2)若$CE的长度为m$,试探索$\odot O与直线AD的位置关系及对应的m$的取值范围.
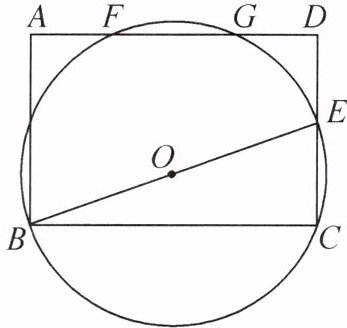

(1)若$CE= 2$,$\odot O交AD于点F$,$G$,求$FG$的长度.
(2)若$CE的长度为m$,试探索$\odot O与直线AD的位置关系及对应的m$的取值范围.


答案:
解: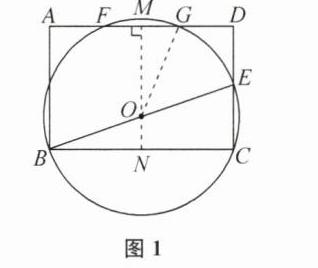
(1) 如图1,过点O作OM⊥FG于点M,延长MO交BC于点N,连接OG.易得四边形MNCD是矩形,所以MN⊥BC,MN=CD=AB=4,所以BN=CN.因为OB=OE,所以ON是△BCE的中位线,所以ON=1/2CE=1,所以OM=MN - ON=3.在Rt△BCE中,BE=√(BC² + CE²)=2√10,所以OG=1/2BE=√10.在Rt△OMG中,MG=√(OG² - OM²)=1,所以FG=2MG=2.
(2) 如图2,当⊙O与AD相切于点M时,连接OM并反向延长交BC于点N.由
(1)易得ON=1/2CE=1/2m,OB=OM=4 - 1/2m,BN=3.在Rt△BON中,ON² + BN²=OB²,即(1/2m)² + 3²=(4 - 1/2m)²,解得m=7/4.易知m的值越大,⊙O的半径r=1/2√(BC² + CE²)=1/2√(36 + m²)越大,⊙O到AD的距离d=4 - 1/2m越小,所以当0<m<7/4时,⊙O与AD相离,当m=7/4时,⊙O与AD相切,当7/4<m<4时,⊙O与AD相交.
解:

(1) 如图1,过点O作OM⊥FG于点M,延长MO交BC于点N,连接OG.易得四边形MNCD是矩形,所以MN⊥BC,MN=CD=AB=4,所以BN=CN.因为OB=OE,所以ON是△BCE的中位线,所以ON=1/2CE=1,所以OM=MN - ON=3.在Rt△BCE中,BE=√(BC² + CE²)=2√10,所以OG=1/2BE=√10.在Rt△OMG中,MG=√(OG² - OM²)=1,所以FG=2MG=2.
(2) 如图2,当⊙O与AD相切于点M时,连接OM并反向延长交BC于点N.由
(1)易得ON=1/2CE=1/2m,OB=OM=4 - 1/2m,BN=3.在Rt△BON中,ON² + BN²=OB²,即(1/2m)² + 3²=(4 - 1/2m)²,解得m=7/4.易知m的值越大,⊙O的半径r=1/2√(BC² + CE²)=1/2√(36 + m²)越大,⊙O到AD的距离d=4 - 1/2m越小,所以当0<m<7/4时,⊙O与AD相离,当m=7/4时,⊙O与AD相切,当7/4<m<4时,⊙O与AD相交.

查看更多完整答案,请扫码查看


