《2025年小题狂做九年级数学上册苏科版提优版》

1. 如图,点 C 在$\widehat {AB}$上,点 D 在半径 OB 上,则下列结论正确的是(B)

A.$∠ACD+\frac {1}{2}∠AOB= 180^{\circ }$
B.$∠ACB+\frac {1}{2}∠AOB= 180^{\circ }$
C.$∠ACB+∠AOB= 180^{\circ }$
D.$∠OAC+∠OBC= 180^{\circ }$
]

答案： B

2. (2024 吉林省中考)如图,四边形 ABCD 内接于$\odot O$.过点 B 作$BE// AD$,交 CD 于点 E.若$∠BEC= 50^{\circ }$,则$∠ABC$的度数是(C)

A.$50^{\circ }$
B.$100^{\circ }$
C.$130^{\circ }$
D.$150^{\circ }$

答案： C

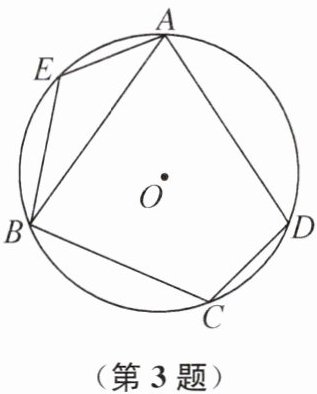
3. 如图,在$\odot O$的内接四边形 ABCD 中,$AB= AD,∠C= 108^{\circ }$,点 E 在$\widehat {AB}$上,则$∠E= $126°.
]

答案： 126 提示:连接AC. 因为AB = AD,所以$\overset{\frown}{AB}=\overset{\frown}{AD}$,所以$∠ACB = ∠ACD = \frac{1}{2}∠BCD = 54^{\circ}$. 因为$∠E + ∠ACB = 180^{\circ}$,所以$∠E = 180^{\circ} - ∠ACB = 126^{\circ}$.

4. 如图,O 为线段 BC 的中点,点 A,C,D 到点 O 的距离相等.若$∠ABC= 40^{\circ }$,则$∠ADC$的度数是$140^{\circ}$.

答案： $140^{\circ}$

5. 如图,将$\odot O$沿弦 AB 折叠,点 C 在$\widehat {AMB}$上,点 D 在$\widehat {AB}$上.若$∠ACB= 70^{\circ }$,则$∠ADB$的度数是$110^{\circ}$.

答案： $110^{\circ}$

6. 如图,四边形 ABCD 内接于$\odot O$,AC,BD 为对角线,$CB= CD,∠CAD= 30^{\circ },∠ACD= 45^{\circ }$,连接 OA,OB,则$∠OAB=$15°.

答案： 15

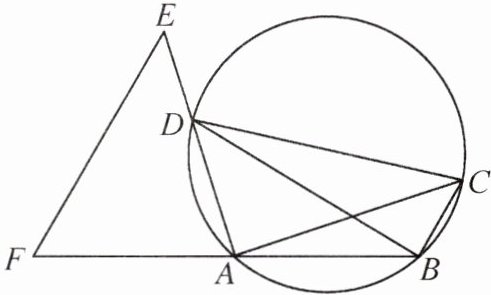
7. (2024 浙江省中考)如图,在圆内接四边形 ABCD 中,$AD＜AC,∠ADC＜∠BAD$,延长 AD 至点 E,使$AE= AC$,延长 BA 至点 F,连接 EF,使$∠AFE= ∠ADC$.
(1)若$∠AFE= 60^{\circ }$,CD 为直径,求$∠ABD$的度数.
(2)求证:①$EF// BC$;②$EF= BD$.
]

答案：
(1)解:因为CD为直径,所以$∠CAD = 90^{\circ}$. 因为$∠AFE = ∠ADC = 60^{\circ}$,所以$∠ACD = 180^{\circ} - ∠CAD - ∠ADC = 30^{\circ}$,所以$∠ABD = ∠ACD = 30^{\circ}$.
(2)证明:①如图,延长AB. 因为四边形ABCD是圆内接四边形,所以$∠CBM = ∠ADC$. 又因为$∠AFE = ∠ADC$,所以$∠AFE = ∠CBM$,所以$EF// BC$.
②过点D作$DG// BC$交$\odot O$于点G,连接AG,CG. 因为$DG// BC$,$∠DGC + ∠BCG = 180^{\circ}$,又因为$∠DGC + ∠DBC = 180^{\circ}$,所以$∠BCG = ∠DBC$,所以$\overset{\frown}{BAG}=\overset{\frown}{DGC}$,所以$\overset{\frown}{BD}=\overset{\frown}{CG}$,所以$BD = CG$. 因为四边形ACGD是圆内接四边形,所以$∠GDE = ∠ACG$. 因为$EF// BC// DG$,所以$∠DEF = ∠GDE$,所以$∠DEF = ∠ACG$. 因为$∠AFE = ∠ADC$,$∠ADC = ∠AGC$,所以$∠AFE = ∠AGC$. 又因为$AE = AC$,所以$\triangle AEF\cong \triangle ACG(AAS)$,所以$EF = CG$,所以$EF = BD$.