第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. (2024 镇江市句容市期中)如图,在一个边长为 m 的正六边形纸板中截去一个边长为 m 的等边三角形后,余下部分的面积与所截去的等边三角形的面积之比为 (
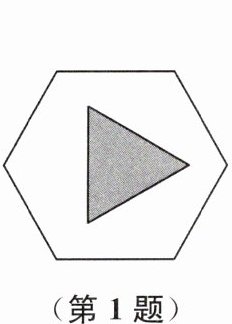
A.3:1
B.4:1
C.5:1
D.6:1
]
C
)
A.3:1
B.4:1
C.5:1
D.6:1
]
答案:
C
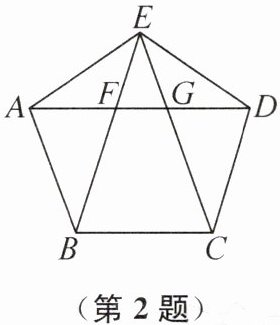
2. 如图,正五边形的五个内角都相等,五条边都相等,连接对角线 AD,BE,CE,线段 AD 分别与 BE 和 CE 相交于点 F,G,给出下列结论:①∠AGC= 108°;②AG= AE;③∠EBC= 2∠BEC;④BF= DE.其中正确的有 (
A.1个
B.2个
C.3个
D.4个
D
)
A.1个
B.2个
C.3个
D.4个
答案:
D
3. 我们知道,除三角形外,其他多边形都不具有稳定性.如图,将正五边形 OABCD 的边 AB 固定,向右推动该正五边形,使得 O 为 AD 的中点,且点 A,B,C,D 在以点 O 为圆心的圆上,过点 C 作⊙O 的切线 EF,则∠BCF 的度数为 (
A.18°
B.30°
C.36°
D.54°
B
)A.18°
B.30°
C.36°
D.54°
答案:
B
4. 如图,A,B,C,D,E 是⊙O 上的五等分点,该图形绕点 O 至少旋转
72
°后与自身重合.
答案:
72
5. 如图,在正方形网格中,每一个小正方形的边长都为 1,点 O,A 都在格点上,以点 O 为圆心,OA 的长为半径作圆.请按要求,只用无刻度的直尺完成以下画图.
(1) 在图 1 中画⊙O 的一个内接正四边形 ABCD,$S_{正四边形ABCD}=$
(2) 在图 2 中画⊙O 的一个内接正六边形 ABCDEF,$S_{正六边形ABCDEF}=$
(1) 在图 1 中画⊙O 的一个内接正四边形 ABCD,$S_{正四边形ABCD}=$
32
;(2) 在图 2 中画⊙O 的一个内接正六边形 ABCDEF,$S_{正六边形ABCDEF}=$
$24\sqrt{3}$
.
答案:
(1) 32
(2) $24\sqrt{3}$
(1) 32
(2) $24\sqrt{3}$
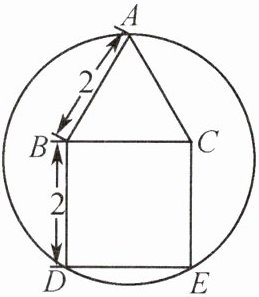
6. 如图,已知多边形 ABDEC 是由边长为 2 的等边三角形 ABC 和正方形 BDEC 组成.若有一圆过 A,D,E 三点,求该圆的半径.
]
]

答案:
过点A作AG⊥DE于点G,交BC于点H,易知圆心在AG上,记为O,连接OD.因为四边形BDEC是正方形,所以BC//DE.因为AG⊥DE,所以AG⊥BC.又因为△ABC为等边三角形,所以BH=CH,∠BAH=∠CAH=30°,所以$BH=CH=\frac{1}{2}AB=1$.由勾股定理,得$AH=\sqrt{AB^2-BH^2}=\sqrt{3}$.设OA=x,则OD=x,$OG=\sqrt{3}+2-x$.在Rt△ODG中,由勾股定理,得$OD^2=OG^2+GD^2$,即$x^2=(\sqrt{3}+2-x)^2+1^2$,解得x=2.所以该圆的半径为2.
1. 半径相等的圆的内接正三角形、正方形和正六边形的边长之比为 (
A.3:2:1
B.$1:\frac{1}{2}:\frac{1}{3}$
C.$\sqrt{3}:\sqrt{2}:1$
D.6:4:3
C
)A.3:2:1
B.$1:\frac{1}{2}:\frac{1}{3}$
C.$\sqrt{3}:\sqrt{2}:1$
D.6:4:3
答案:
C 提示:如图,设⊙O的半径为r.图1中,∠OAH=30°,$OH=\frac{1}{2}r$,$AH=\frac{\sqrt{3}}{2}r$,$AB=\sqrt{3}r$;图2中,∠AOB=90°,OA=OB=r,$AB=\sqrt{2}r$;图3中,∠AOH=30°,$AH=\frac{1}{2}r$,AB=r.所以边长之比为$\sqrt{3}r:\sqrt{2}r:r=\sqrt{3}:\sqrt{2}:1$.
查看更多完整答案,请扫码查看


