第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图,在半径为 10 的扇形 OAB 中,∠AOB= 90°,C 为$\overset{\frown}{AB}$上一点,CD⊥OA,CE⊥OB,垂足分别为 D,E. 若∠CDE= 36°,则图中阴影部分的面积为(
A.10π
B.9π
C.8π
D.6π
A
)A.10π
B.9π
C.8π
D.6π
答案:
A
2. 将一张圆心角为 30°的扇形纸板和一张圆形纸板分别按如图所示的方式剪出一个边长都为 1 的正三角形,则扇形和圆形纸板的面积之比是(
A.1:1
B.3:2
C.$\sqrt{3}:2$
D.$2:\sqrt{3}$
A
)A.1:1
B.3:2
C.$\sqrt{3}:2$
D.$2:\sqrt{3}$
答案:
A
3. (2024 镇江市中考)如图,四边形 ABCD 为平行四边形,以点 A 为圆心,AB 长为半径画弧,交边 BC 于点 E,连接 AE,AB= 1,∠D= 60°,则$\overset{\frown}{BE}的长l=$
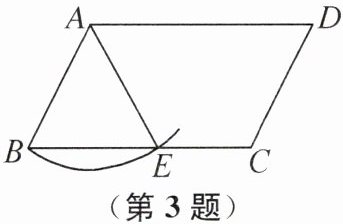
$\frac{\pi}{3}$
(结果保留 π).
答案:
$\frac{\pi}{3}$
4. 如图,在矩形 ABCD 中,AB= 2BC= 2. 将线段 AB 绕点 A 按逆时针方向旋转,使得点 B 落在边 CD 上的点 B'处,则线段 AB 扫过的面积为
$\frac{\pi}{3}$
.
答案:
$\frac{\pi}{3}$ 提示:因为$AB = 2BC = 2$,所以$BC = 1$。在矩形$ABCD$中,$AD = BC = 1$,$\angle D = \angle DAB = 90^{\circ}$。由旋转可知$AB' = AB = 2$,所以$AB' = 2AD$,所以$\angle DB'A = 30^{\circ}$。因为$DC// AB$,所以$\angle BAB' = \angle DB'A = 30^{\circ}$。所以线段$AB$扫过的区域面积为$\frac{30^{\circ}×\pi×2^2}{360^{\circ}}=\frac{\pi}{3}$。
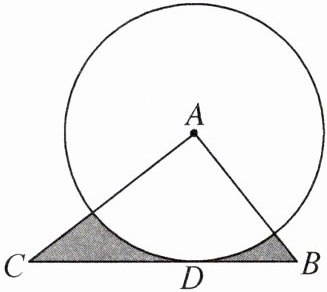
5. (2024 南通市中考)如图,△ABC 中,AB= 3,AC= 4,BC= 5,⊙A 与 BC 相切于点 D.
(1) 求图中阴影部分的面积;
(2) 设⊙A 上有一动点 P,连接 CP,BP. 当 CP 的长最大时,求 BP 的长.
(1) 求图中阴影部分的面积;
(2) 设⊙A 上有一动点 P,连接 CP,BP. 当 CP 的长最大时,求 BP 的长.

答案:
(1)连接$AD$。因为$AB = 3$,$AC = 4$,$BC = 5$,所以$AC^2 + AB^2 = BC^2$,所以$\angle BAC = 90^{\circ}$。因为$\odot A$与$BC$相切于点$D$,所以$AD\perp BC$。由等积法,得$AD = \frac{AC\cdot AB}{BC}=\frac{4×3}{5}=\frac{12}{5}$,所以$S_{阴影}=S_{\triangle ABC}-S_{扇形}=\frac{1}{2}AB\cdot AC-\frac{90^{\circ}×\pi× AD^2}{360^{\circ}}=6-\frac{36}{25}\pi$。
(2)如图,延长$CA$交$\odot A$于点$P$,连接$BP$。易知当$C$,$A$,$P$三点共线时,$CP$的长最大,则$\angle PAB = 90^{\circ}$。因为$AP = \frac{12}{5}$,$AB = 3$,所以$BP = \sqrt{AP^2 + AB^2}=\frac{3\sqrt{41}}{5}$。

(1)连接$AD$。因为$AB = 3$,$AC = 4$,$BC = 5$,所以$AC^2 + AB^2 = BC^2$,所以$\angle BAC = 90^{\circ}$。因为$\odot A$与$BC$相切于点$D$,所以$AD\perp BC$。由等积法,得$AD = \frac{AC\cdot AB}{BC}=\frac{4×3}{5}=\frac{12}{5}$,所以$S_{阴影}=S_{\triangle ABC}-S_{扇形}=\frac{1}{2}AB\cdot AC-\frac{90^{\circ}×\pi× AD^2}{360^{\circ}}=6-\frac{36}{25}\pi$。
(2)如图,延长$CA$交$\odot A$于点$P$,连接$BP$。易知当$C$,$A$,$P$三点共线时,$CP$的长最大,则$\angle PAB = 90^{\circ}$。因为$AP = \frac{12}{5}$,$AB = 3$,所以$BP = \sqrt{AP^2 + AB^2}=\frac{3\sqrt{41}}{5}$。

6. (2024 辽宁省中考)如图,⊙O 是△ABC 的外接圆,AB 是⊙O 的直径,点 D 在$\overset{\frown}{BC}$上,$\overset{\frown}{AC}= \overset{\frown}{BD}$,点 E 在 BA 的延长线上,∠CEA= ∠CAD.
(1) 如图 1,求证:CE 是⊙O 的切线;
(2) 如图 2,若∠CEA= 2∠DAB,OA= 8,求$\overset{\frown}{BD}$的长.
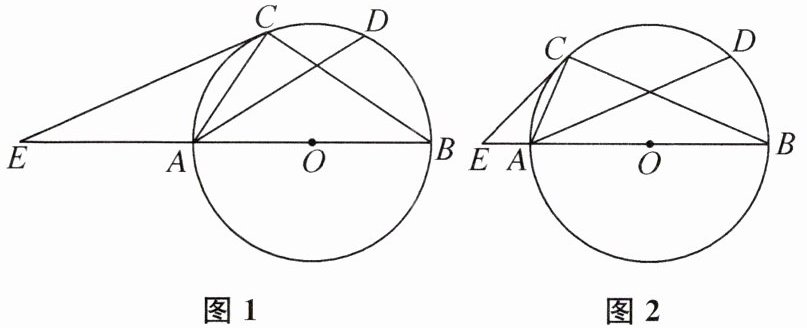
(1) 如图 1,求证:CE 是⊙O 的切线;
(2) 如图 2,若∠CEA= 2∠DAB,OA= 8,求$\overset{\frown}{BD}$的长.
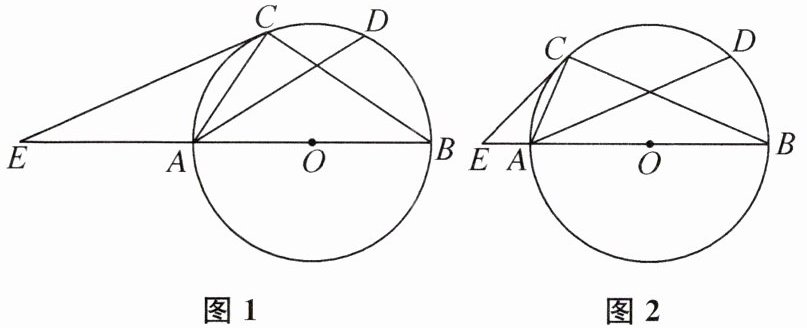
答案:
(1)证明:如图1,连接$OC$,$OD$,因为$\widehat{AC}=\widehat{BD}$,所以$\angle AOC = \angle DOB$,$\angle COD = 2\angle CAD$,所以$2\angle AOC + 2\angle CAD = 180^{\circ}$,即$\angle AOC + \angle CAD = 90^{\circ}$。又因为$\angle CEA = \angle CAD$,所以$\angle AOC + \angle CEA = 90^{\circ}$,所以$\angle OCE = 90^{\circ}$,又因为$OC$是$\odot O$的半径,所以$CE$是$\odot O$的切线。
(2)解:如图2,连接$OD$,设$\angle DAB = x$。因为$\angle CEA = 2\angle DAB$,所以$\angle CEA = 2x$。因为$\angle CEA = \angle CAD$,所以$\angle CAD = 2x$。因为$\widehat{AC}=\widehat{BD}$,所以$\angle ABC = \angle DAB = x$。因为$AB$是$\odot O$的直径,所以$\angle ACB = 90^{\circ}$,所以$\angle ABC + \angle BAC = 90^{\circ}$,所以$x + 2x + x = 90^{\circ}$,解得$x = 22.5^{\circ}$,即$\angle DAB = 22.5^{\circ}$,所以$\angle BOD = 2\angle DAB = 45^{\circ}$。因为$OA = 8$,所以$\widehat{BD}$的长为$\frac{45\pi×8}{180}=2\pi$。


(1)证明:如图1,连接$OC$,$OD$,因为$\widehat{AC}=\widehat{BD}$,所以$\angle AOC = \angle DOB$,$\angle COD = 2\angle CAD$,所以$2\angle AOC + 2\angle CAD = 180^{\circ}$,即$\angle AOC + \angle CAD = 90^{\circ}$。又因为$\angle CEA = \angle CAD$,所以$\angle AOC + \angle CEA = 90^{\circ}$,所以$\angle OCE = 90^{\circ}$,又因为$OC$是$\odot O$的半径,所以$CE$是$\odot O$的切线。
(2)解:如图2,连接$OD$,设$\angle DAB = x$。因为$\angle CEA = 2\angle DAB$,所以$\angle CEA = 2x$。因为$\angle CEA = \angle CAD$,所以$\angle CAD = 2x$。因为$\widehat{AC}=\widehat{BD}$,所以$\angle ABC = \angle DAB = x$。因为$AB$是$\odot O$的直径,所以$\angle ACB = 90^{\circ}$,所以$\angle ABC + \angle BAC = 90^{\circ}$,所以$x + 2x + x = 90^{\circ}$,解得$x = 22.5^{\circ}$,即$\angle DAB = 22.5^{\circ}$,所以$\angle BOD = 2\angle DAB = 45^{\circ}$。因为$OA = 8$,所以$\widehat{BD}$的长为$\frac{45\pi×8}{180}=2\pi$。


查看更多完整答案,请扫码查看


