第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1.(2024 南京市建邺区期中)用配方法解方程 $x^{2}-4x-1= 0$,下列变形正确的是(
A.$(x-2)^{2}= 5$
B.$(x-4)^{2}= 5$
C.$(x-4)^{2}= 3$
D.$(x-2)^{2}= 3$
A
)A.$(x-2)^{2}= 5$
B.$(x-4)^{2}= 5$
C.$(x-4)^{2}= 3$
D.$(x-2)^{2}= 3$
答案:
A
2.(2024 河北省中考)淇淇在计算正数 $a$ 的平方时,误算成 $a$ 与 2 的积,求得的答案比正确答案小 1,则 $a$ 的值为(
A.1
B.$\sqrt{2}-1$
C.$\sqrt{2}+1$
D.1 或$\sqrt{2}+1$
C
)A.1
B.$\sqrt{2}-1$
C.$\sqrt{2}+1$
D.1 或$\sqrt{2}+1$
答案:
C
3. 若 $a$,$b$,$c$ 分别是$\triangle ABC$ 的三条边长,且满足 $a^{2}+2ab= c^{2}+2bc$,则$\triangle ABC$ 是(
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等边三角形
B
)A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等边三角形
答案:
B 提示:配方,得$a^{2}+2ab+b^{2}=c^{2}+2bc+b^{2}$,即$(a+b)^{2}=(c+b)^{2}$.根据题意,可知a,b,c均大于0,所以$a+b=b+c$,所以$a=c$,所以$\triangle ABC$是等腰三角形.
4. 若一元二次方程 $x^{2}-4x+3= 0$ 配方为 $(x-2)^{2}= k$,则 $k$ 的值是______
1
.
答案:
1
5. 若一元二次方程 $x^{2}-ax+b= 0$ 配方后为 $(x-4)^{2}= 3$,则 $a+b= $
21
.
答案:
21
6. 填空:
(1)$x^{2}-12x+$
(2)$x^{2}+6x+$
(3)$x^{2}-3x+$
(4)$x^{2}-\frac{5}{2}x+$
(1)$x^{2}-12x+$
36
$=(x-$6
$)^{2}$;(2)$x^{2}+6x+$
9
$=(x+$3
$)^{2}$;(3)$x^{2}-3x+$
$\frac{9}{4}$
$=(x-$$\frac{3}{2}$
$)^{2}$;(4)$x^{2}-\frac{5}{2}x+$
$\frac{25}{16}$
$=(x-$$\frac{5}{4}$
$)^{2}$.
答案:
(1) 36 6
(2) 9 3
(3)$\frac{9}{4}$ $\frac{3}{2}$
(4)$\frac{25}{16}$ $\frac{5}{4}$
(1) 36 6
(2) 9 3
(3)$\frac{9}{4}$ $\frac{3}{2}$
(4)$\frac{25}{16}$ $\frac{5}{4}$
7. 用配方法解下列方程:
(1)$x^{2}+3x-1= 0$;
(2)$x^{2}-\frac{1}{6}x-\frac{1}{3}= 0$.
(1)$x^{2}+3x-1= 0$;
(2)$x^{2}-\frac{1}{6}x-\frac{1}{3}= 0$.
答案:
解:
(1) 移项,得$x^{2}+3x=1$.配方,得$x^{2}+3x+\left(\frac{3}{2}\right)^{2}=1+\left(\frac{3}{2}\right)^{2}$,即$\left(x+\frac{3}{2}\right)^{2}=\frac{13}{4}$.直接开平方,得$x+\frac{3}{2}=\pm \frac{\sqrt{13}}{2}$.所以$x_{1}=\frac{-3+\sqrt{13}}{2}$,$x_{2}=\frac{-3-\sqrt{13}}{2}$.
(2) 移项,得$x^{2}-\frac{1}{6}x=\frac{1}{3}$.配方,得$x^{2}-\frac{1}{6}x+\frac{1}{144}=\frac{1}{3}+\frac{1}{144}$,即$\left(x-\frac{1}{12}\right)^{2}=\frac{49}{144}$.直接开平方,得$x-\frac{1}{12}=\pm \frac{7}{12}$.所以$x_{1}=\frac{2}{3}$,$x_{2}=-\frac{1}{2}$.
(1) 移项,得$x^{2}+3x=1$.配方,得$x^{2}+3x+\left(\frac{3}{2}\right)^{2}=1+\left(\frac{3}{2}\right)^{2}$,即$\left(x+\frac{3}{2}\right)^{2}=\frac{13}{4}$.直接开平方,得$x+\frac{3}{2}=\pm \frac{\sqrt{13}}{2}$.所以$x_{1}=\frac{-3+\sqrt{13}}{2}$,$x_{2}=\frac{-3-\sqrt{13}}{2}$.
(2) 移项,得$x^{2}-\frac{1}{6}x=\frac{1}{3}$.配方,得$x^{2}-\frac{1}{6}x+\frac{1}{144}=\frac{1}{3}+\frac{1}{144}$,即$\left(x-\frac{1}{12}\right)^{2}=\frac{49}{144}$.直接开平方,得$x-\frac{1}{12}=\pm \frac{7}{12}$.所以$x_{1}=\frac{2}{3}$,$x_{2}=-\frac{1}{2}$.
8. 我们知道:$x^{2}-6x= (x^{2}-6x+9)-9= (x-3)^{2}-9$;$-x^{2}+10x= -(x^{2}-10x+25)+25= -(x-5)^{2}+25$. 这一种方法称为配方法,利用配方法解答以下各题:
(1)填空:$a^{2}-4a=$
(2)探究:当 $a$ 取不同的实数时,代数式 $a^{2}-4a$ 的值是否存在最小值?请说明理由.
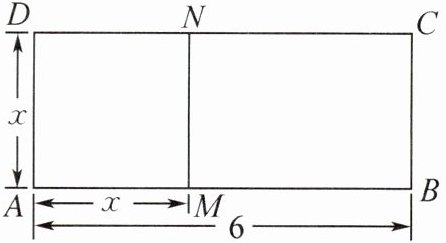
(3)应用:如图,已知线段 $AB= 6$,$M$ 是 $AB$ 上的一个动点,设 $AM= x$,以 $AM$ 为一边作正方形 $AMND$,再以 $MB$,$MN$ 为一组邻边作长方形 $MBCN$. 当点 $M$ 在线段 $AB$ 上运动时,长方形 $MBCN$ 的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
]
(1)填空:$a^{2}-4a=$
$(a^{2}-4a+4)-4$
$=$$(a-2)^{2}-4$
;$-a^{2}+12a=$$-(a^{2}-12a+36)+36$
$=$$-(a-6)^{2}+36$
.(2)探究:当 $a$ 取不同的实数时,代数式 $a^{2}-4a$ 的值是否存在最小值?请说明理由.
存在,理由如下:因为$a^{2}-4a=(a-2)^{2}-4\geq -4$,所以当$a=2$时,代数式$a^{2}-4a$取得最小值,最小值为-4.所以当a取不同的实数时,$a^{2}-4a$存在最小值.
(3)应用:如图,已知线段 $AB= 6$,$M$ 是 $AB$ 上的一个动点,设 $AM= x$,以 $AM$ 为一边作正方形 $AMND$,再以 $MB$,$MN$ 为一组邻边作长方形 $MBCN$. 当点 $M$ 在线段 $AB$ 上运动时,长方形 $MBCN$ 的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
存在.根据题意,得$S=x(6-x)=-x^{2}+6x=-(x-3)^{2}+9\leq 9$.当$x=3$时,S取最大值,最大值为9.
]

答案:
解:
(1)$(a^{2}-4a+4)-4$ $(a-2)^{2}-4$
$-(a^{2}-12a+36)+36$ $-(a-6)^{2}+36$
(2) 存在,理由如下:
因为$a^{2}-4a=(a-2)^{2}-4\geq -4$,所以当$a=2$时,代数式$a^{2}-4a$取得最小值,最小值为-4.所以当a取不同的实数时,$a^{2}-4a$存在最小值.
(3) 存在.根据题意,得$S=x(6-x)=-x^{2}+6x=-(x-3)^{2}+9\leq 9$.当$x=3$时,S取最大值,最大值为9.
(1)$(a^{2}-4a+4)-4$ $(a-2)^{2}-4$
$-(a^{2}-12a+36)+36$ $-(a-6)^{2}+36$
(2) 存在,理由如下:
因为$a^{2}-4a=(a-2)^{2}-4\geq -4$,所以当$a=2$时,代数式$a^{2}-4a$取得最小值,最小值为-4.所以当a取不同的实数时,$a^{2}-4a$存在最小值.
(3) 存在.根据题意,得$S=x(6-x)=-x^{2}+6x=-(x-3)^{2}+9\leq 9$.当$x=3$时,S取最大值,最大值为9.
查看更多完整答案,请扫码查看


