第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图,在△ABC中,AB= AC,AD是∠BAC的平分线,EF是AC的垂直平分线,交AD于点O. 若OA= 3,则△ABC外接圆的面积为 (
A.3π
B.4π
C.6π
D.9π
D
)A.3π
B.4π
C.6π
D.9π
答案:
D
2. 如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为 (
A.3个
B.4个
C.5个
D.6个
D
)A.3个
B.4个
C.5个
D.6个
答案:
D
3. 如图,⊙O是锐角三角形ABC的外接圆,OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D,E,F,连接DE,EF,FD. 若DE+DF= 13/2,△ABC的周长为21,则EF的长为 (
A.8
B.4
C.7/2
D.3
B
)A.8
B.4
C.7/2
D.3
答案:
B 提示:因为OD⊥AB,OE⊥BC,OF⊥AC,所以AD=BD,AF=CF,BE=CE,所以DE,DF,EF 是△ABC的中位线,所以$DE=\frac{1}{2}AC$,$DF=\frac{1}{2}BC$,$EF=\frac{1}{2}AB$,所以$DE+DF+EF=\frac{1}{2}(AB+BC+AC)=\frac{1}{2}×21=\frac{21}{2}$.因为$DE+DF=\frac{13}{2}$,所以EF=4.
4. 如图,已知点E是△ABC的外心,P,Q分别是AB,AC的中点,连接EP,EQ交BC于点F,D,若BF= 5,DF= 3,CD= 4,则△ABC的面积为 (
A.18
B.24
C.30
D.36
B
)A.18
B.24
C.30
D.36
答案:
B
5. (2024 宿迁市宿城区期中)设x,y是一个直角三角形两条直角边的长,且$(x^2+y^2)·(x^2+y^2-1)= 56,$则这个直角三角形的外接圆面积为
2π
.
答案:
2π
6. 根据三角形外心的概念,我们可引入一个新定义:到三角形的两个顶点距离相等的点,叫作此三角形的准外心. 根据准外心的定义,探究如下问题:如图,在Rt△ABC中,∠A= 90°,BC= 10,AB= 6,如果准外心P在边AC上,那么PA的长为
4或$\frac{7}{4}$
.
答案:
4或$\frac{7}{4}$ 提示:在Rt△ABC中,由勾股定理,得$AC=\sqrt{BC^2-AB^2}=8$.分三种情况讨论:若PB=PC,连接PB,设PA=x,则PB=PC=8−x.在Rt△PAB中,因为$PB^2=PA^2+AB^2$,所以$(8-x)^2=x^2+6^2$,解得$x=\frac{7}{4}$,即$PA=\frac{7}{4}$.若PA=PC,则PA=4.若PA=PB,因为在Rt△PAB中,PB是斜边,所以此种情况不存在
7. (2024 南京市鼓楼区期中)尺规作图:已知线段AB和⊙O,将线段AB沿某条直线翻折后,A,B两点恰好落在⊙O上,请按照下列要求分别作出翻折后的线段A'B'.(保留作图痕迹,并写出必要的文字说明)
(1)如图1,AB的长度等于⊙O的直径;
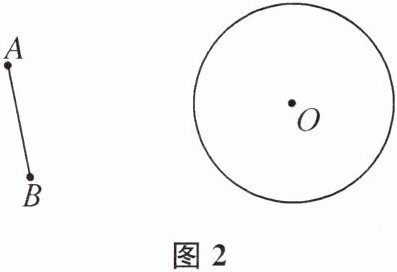
(2)如图2,AB的长度小于⊙O的直径.
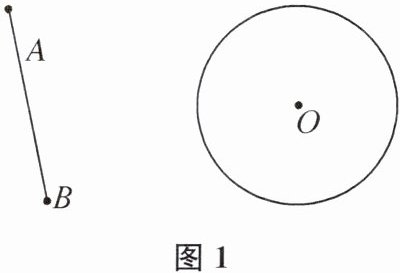
(1)如图1,AB的长度等于⊙O的直径;
(2)如图2,AB的长度小于⊙O的直径.


答案:
解:
(1)如图1,作法如下:①作线段AB的垂直平分线,取线段AB 的中点O';②以点O'为圆心,$\frac{1}{2}AB$为半径作⊙O',连接OO';③作OO'的垂直平分线l,作点B关于直线l的对称点B';④连接B'O并延长交⊙O于点A',线段A'B'即为所求.
(2)作法如下:①作线段AB的垂直平分线m,在直线m 上取点O',使得O'A等于⊙O的半径长,作⊙O的等圆⊙O';②连接OO',作OO'的垂直平分线l,作点B关于直线l的对称点B',点A关于直线l的对称点A';③连接A'B',线段A'B'即为所求.当点O'位于AB的右侧时,如图2,线段A'B'即为所求. 当点O'位于AB的左侧时,如图3,线段A'B'即为所求.
当点O'位于AB的左侧时,如图3,线段A'B'即为所求. 
解:
(1)如图1,作法如下:①作线段AB的垂直平分线,取线段AB 的中点O';②以点O'为圆心,$\frac{1}{2}AB$为半径作⊙O',连接OO';③作OO'的垂直平分线l,作点B关于直线l的对称点B';④连接B'O并延长交⊙O于点A',线段A'B'即为所求.

(2)作法如下:①作线段AB的垂直平分线m,在直线m 上取点O',使得O'A等于⊙O的半径长,作⊙O的等圆⊙O';②连接OO',作OO'的垂直平分线l,作点B关于直线l的对称点B',点A关于直线l的对称点A';③连接A'B',线段A'B'即为所求.当点O'位于AB的右侧时,如图2,线段A'B'即为所求.
 当点O'位于AB的左侧时,如图3,线段A'B'即为所求.
当点O'位于AB的左侧时,如图3,线段A'B'即为所求. 
查看更多完整答案,请扫码查看


