《2025年小题狂做九年级数学上册苏科版提优版》

1. 如图,A,B,C 是$\odot O$上的点,且$\angle ACB= 140^{\circ}$.在这个图中,画出下列度数的圆周角:$40^{\circ},50^{\circ},90^{\circ},140^{\circ}$,其中仅用无刻度的直尺就能画出的有(D)
A.1个
B.2个
C.3个
D.4个

答案： D

2. (2024 湖北省中考)如图,AB 是半圆 O 的直径,C 为半圆 O 上一点,以点 B 为圆心,适当长为半径画弧,交 BA 于点 M,交 BC 于点 N,分别以点 M,N 为圆心,大于$\frac{1}{2}MN$的长为半径画弧,两弧在$\angle ABC$的内部相交于点 D,画射线 BD,连接 AC.若$\angle CAB= 50^{\circ}$,则$\angle CBD$的度数是(C)

A.$30^{\circ}$
B.$25^{\circ}$
C.$20^{\circ}$
D.$15^{\circ}$

答案： C

3. (2024 常州市中考)如图,AB 是$\odot O$的直径,CD 是$\odot O$的弦,连接 AD,BC,BD.若$\angle BCD= 20^{\circ}$,则$\angle ABD= $70°.

答案： 70

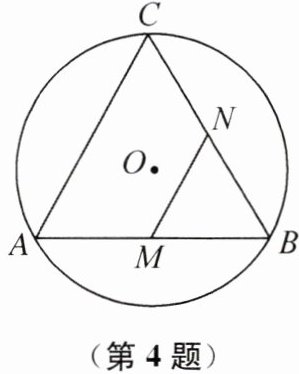
4. 如图,AB 是$\odot O$的弦,$AB= 2\sqrt{3}$,C 是$\odot O$上的一个动点,且$\angle ACB= 60^{\circ}$.若 M,N 分别是弦 AB,BC 的中点,则 MN 长的最大值是______2.

答案： 2 提示:如图,连接 AO 并延长,交⊙O 于点 D,连接 BD. 因为 M,N 分别是弦 AB,BC 的中点,所以 MN 是△ABC 的中位线,所以 MN=$\frac{1}{2}$AC,所以当 AC 的长最大时,MN 的长最大. 因为 C 是⊙O 上的一个动点,且∠ACB=60°,所以当点 C 运动到点 D 处时,AC 的长最大,最大值即为⊙O 的直径 AD 的长. 在△ABD 中,易知∠ADB=60°,因为 AD 为⊙O 的直径,所以∠ABD=90°,所以∠BAD=30°,所以 BD=$\frac{1}{2}$AD,由勾股定理,得 BD²+AB²=AD²,即$(\frac{1}{2}AD)^{2}+(2\sqrt{3})^{2}=(AD)^{2}$,解得 AD=4(负值已舍),所以 MN 长的最大值为 2.

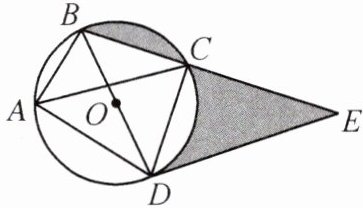
5. 如图,四边形 ABCD 内接于$\odot O$,BD 为$\odot O$的直径,AC 平分$\angle BAD$,$CD= 2\sqrt{2}$,点 E 在 BC 的延长线上,连接 DE.
(1)求直径 BD 的长；
(2)若$BE= 5\sqrt{2}$,计算图中阴影部分的面积.

答案：
(1)因为 AC 平分∠BAD,所以∠BAC=∠CAD. 因为在同圆中相等的圆周角所对的弧、弦均相等,所以 CB=CD=2$\sqrt{2}$. 因为 BD 是⊙O 的直径,所以∠BCD=90°,所以直径 BD 的长为$\sqrt{2}$CD=4.
(2)因为 CB=CD=2$\sqrt{2}$,BE=5$\sqrt{2}$,所以 CE=BE - CB=3$\sqrt{2}$. 由
(1)可知,∠DCE=90°,C 是半圆的中点,所以由圆的对称性可知,$S_{阴影}=S_{\triangle DCE}=\frac{1}{2}CD\cdot CE=\frac{1}{2}×2\sqrt{2}×3\sqrt{2}=6$.

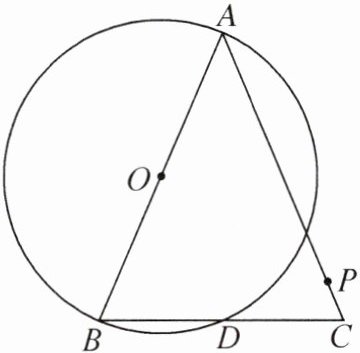
6. 如图,在$\triangle ABC$中,$AB= AC$,以 AB 为直径的$\odot O$经过点 D,点 P 是边 AC 上一点(不与点 A,C 重合).请仅用无刻度直尺按要求作图,保留作图痕迹,不写作法.
(1)过点 A 作一条直线,将$\triangle ABC$分成面积相等的两部分；
(2)在边 AB 上找一点$P'$,使得$BP'= CP$.

答案：

(1)如图,直线 AD 为所求.
(2)如图,点 P'为所求.