《2025年小题狂做九年级数学上册苏科版提优版》

1.(2024 长沙市中考)如图,在$\odot O$中,弦 AB 的长为 8,圆心 O 到 AB 的距离$OE= 4$,则$\odot O$的半径长为(B)

A.4
B.$4\sqrt {2}$
C.5
D.$5\sqrt {2}$

答案： B

2. 如图,一个纵截面为半圆的容器水平放置,然后向其中倒入部分液体,测得数据如图(单位:cm),则液面宽度 AB 的长度为(D)
A.8 cm
B.4 cm
C.$4\sqrt {3}cm$
D.$8\sqrt {3}cm$

答案： D

3. 如图,在$Rt\triangle ABC$中,$∠ACB= 90^{\circ }$,P 是$\widehat {AC}$的中点,连接 BP 交 AC 于点 D. 若半圆的圆心为 O,点 D,E 关于圆心 O 对称,则图中的两个阴影部分的面积$S_{1},S_{2}$之间的关系是(C)
A.$S_{1}\lt S_{2}$
B.$S_{1}＞S_{2}$
C.$S_{1}= S_{2}$
D.不确定

答案： C

4. 如图,AB 是$\odot O$的弦,AB 的长为 4,P 是$\odot O$上的一个动点(不与点 A,B 重合).过点 O 分别作$OC⊥AP$于点 C,$OD⊥PB$于点 D,则 CD 的长为2.

答案： 2

5. 如图,已知 AB 是$\odot O$的直径,弦$CD⊥AB$于点 H. 若$AB= 10,CD= 8$,则图中阴影部分的面积为20.

答案： 20

6.(2024 盐城市盐城开发区期中)如图,某桨轮船的轮子被水面截得的弦 AB 长 8 m,设圆心为 O,$OC⊥AB$交水面 AB 于点 D,轮子的吃水深度 CD 为 2 m,求该桨轮船的轮子直径.

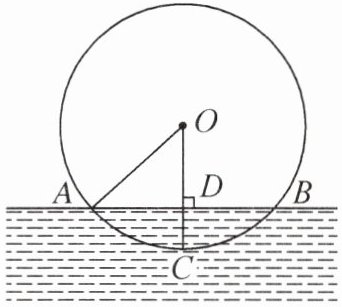
答案： 解:设半径为r m,则OA=OC=r m,所以OD=(r-2)m.因为AB=8 m,OC⊥AB,所以AD=4 m.在Rt△ODA中,由勾股定理,得OA²=OD²+AD²,即r²=(r-2)²+4²,解得r=5,则该桨轮船的轮子直径为10 m.

7. 如图,在以点 O 为圆心的两个同心圆中,大圆的弦 AB 交小圆于点 C,D.
(1) 求证:$AC= BD;$
(2) 若$AC= 3$,大圆和小圆的半径分别为 6 和 4,则 CD 的长是______$\frac{11}{3}$.

答案： （1）证明:过点O作OE⊥AB于点E,则AE=BE,CE=DE,所以AE - CE=BE - DE,即AC=BD.（2）$\frac{11}{3}$ 提示:连接OC.在Rt△AOE中,由勾股定理,得OE²=AO² - AE².在Rt△COE中,由勾股定理,得OE²=OC² - CE².所以OC² - CE²=AO² - AE²,即4² - CE²=6² - (3 + CE)²,解得CE=$\frac{11}{6}$.所以CD=2CE=$\frac{11}{3}$.