《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

12. 在正方形 $ ABCD $ 中，点 $ E $ 在边 $ DC $ 上， $ DE = 2,EC = 1 $。把线段 $ AE $ 绕点 $ A $ 旋转，使点 $ E $ 落在直线 $ BC $ 上的点 $ F $ 处，则 $ F,C $ 两点间的距离为______。

答案： 1或5

13. 在平面直角坐标系 $ xOy $ 中，对于任意三点 $ A,B,C $ 的“矩面积”，给出如下定义：“水平底” $ a $：任意两点横坐标差的最大值，“铅垂高” $ h $：任意两点纵坐标差的最大值，则“矩面积” $ S = ah $。例如：三点坐标分别为 $ A(1,2) $， $ B(-3,1) $， $ C(2,-2) $，则“水平底” $ a = 5 $，“铅垂高” $ h = 4 $，“矩面积” $ S = ah = 20 $。若 $ D(1,2) $， $ E(-2,1) $， $ F(0,t) $ 三点的“矩面积”为 $ 18 $，则 $ t $ 的值为______。

答案： −4或7

14. 在 $ \triangle ABC $ 中， $ AB = AC = 12\mathrm{cm},BC = 6\mathrm{cm} $， $ D $ 为 $ BC $ 的中点，动点 $ P $ 从点 $ B $ 出发，以每秒 $ 1\mathrm{cm} $ 的速度沿 $ B\rightarrow A\rightarrow C $ 的方向运动，设运动的时间为 $ t $ 秒，过 $ D,P $ 两点的直线将 $ \triangle ABC $ 的周长分成两个部分，使其中一部分是另一部分的 $ 2 $ 倍，那么 $ t $ 的值为______。

答案： 7或17

15. 对于实数 $ a,b $，定义符号 $ \min\{a,b\} $，其意义为：当 $ a\geq b $ 时， $ \min\{a,b\}=b $；当 $ a ＜ b $ 时， $ \min\{a,b\}=a $。例如： $ \min\{2,-1\}=-1 $，若关于 $ x $ 的函数 $ y=\min\{2x - 1,-x + 3\} $，则该函数的最大值为______。

答案： $\frac{5}{3}$

16. 如图，在梯形 $ ABCD $ 中， $ AD// BC,\angle ABC = 90^{\circ},AD = AB = 6,BC = 14 $，点 $ M $ 是线段 $ BC $ 上一定点，且 $ MC = 8 $。动点 $ P $ 从点 $ C $ 出发沿 $ C\rightarrow D\rightarrow A\rightarrow B $ 的路线运动，运动到点 $ B $ 停止。在点 $ P $ 的运动过程中，使 $ \triangle PMC $ 为等腰三角形的点 $ P $ 有______个。

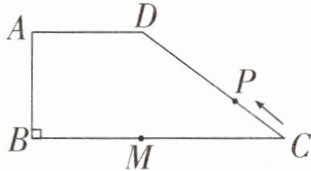
答案： 4

17. 如图①，过 $ \triangle ABC $ 的顶点 $ A $ 分别作对边 $ BC $ 上的高 $ AD $ 和中线 $ AE $，点 $ D $ 是垂足，点 $ E $ 是 $ BC $ 的中点，规定 $ \lambda_{A}=\frac{DE}{BE} $。特别地，当点 $ D,E $ 重合时，规定 $ \lambda_{A}=0 $。另外，对 $ \lambda_{B},\lambda_{C} $ 作类似的规定。
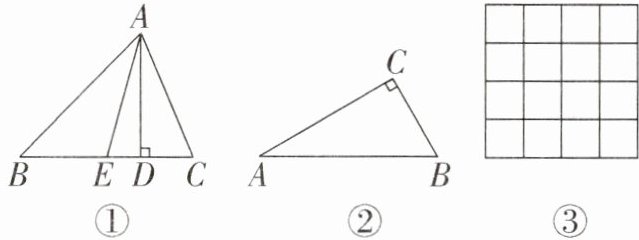
(1) 如图②，已知在 $ \mathrm{Rt}\triangle ABC $ 中， $ \angle A = 30^{\circ} $，求 $ \lambda_{A},\lambda_{C} $。
(2) 在如图③所示的每个小正方形边长为 $ 1 $ 的 $ 4×4 $ 方格纸上，画一个 $ \triangle ABC $，使其顶点在格点（格点即每个小正方形的顶点）上，且 $ \lambda_{A}=2 $，面积也为 $ 2 $。
(3) 判断下列三个命题的真假。（真命题画“$ \surd $”，假命题画“$ × $”）
① 若在 $ \triangle ABC $ 中， $ \lambda_{A}＜1 $，则 $ \triangle ABC $ 为锐角三角形。（ ）
② 若在 $ \triangle ABC $ 中， $ \lambda_{A}=1 $，则 $ \triangle ABC $ 为直角三角形。（ ）
③ 若在 $ \triangle ABC $ 中， $ \lambda_{A}＞1 $，则 $ \triangle ABC $ 为钝角三角形。（ ）

答案：

(1)如图,作CD⊥AB,垂足为D，作中线CE,AF,

∴$\lambda_A$=$\frac{CF}{BF}$=1.
∵在Rt△ABC中,∠CAB=30°,
∴AE=CE=BE,∠CEB=60°,
∴△CEB是等边三角形.
∵CD⊥AB,
∴ED=BD,
∴AE=2DE,
∴$\lambda_C$=$\frac{DE}{AE}$=$\frac{1}{2}$
(2)如图所示.(画法不唯一)

(3)①×　②√　③√