第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
11. 如图,$ l_1 // l_2 $,等边△ABC顶点A,B分别在$ l_1 $,$ l_2 $上,$ ∠2 = 45° $,则∠1度数为________.


答案:
$15^{\circ}$
12. 在△ABC中,$ AB = AC = 5 $,$ BC = 6 $.若点P在边AC上移动,则BP的最小值是________.
答案:
4.8
13. 已知两线段的长分别是5 cm,3 cm,则第三条线段长是________cm时,这三条线段构成直角三角形.
答案:
4 或 $ \sqrt{34} $
14. 如图,在△ABC中,$ AD ⊥ BC $,AE平分∠BAC,若$ ∠1 = 30° $,$ ∠2 = 20° $,则$ ∠B = $________.


答案:
$ 50^{\circ} $
15. 已知a,b,c是△ABC的三边的长,b,c满足$ (b - 2)^2 + |c - 3| = 0 $,且a为方程$ |x - 4| = 2 $的解,则△ABC的周长为________,△ABC的形状为________.
答案:
7 等腰三角形
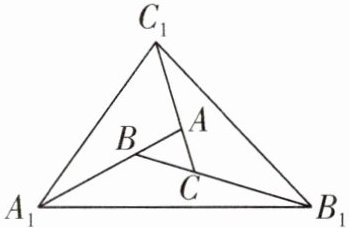
16. 如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB,BC,CA至点$ A_1 $,$ B_1 $,$ C_1 $,使得$ A_1B = 2AB $,$ B_1C = 2BC $,$ C_1A = 2CA $,顺次连接$ A_1 $,$ B_1 $,$ C_1 $,得到$ △A_1B_1C_1 $,记其面积为$ S_1 $;第二次操作,分别延长$ A_1B_1 $,$ B_1C_1 $,$ C_1A_1 $至点$ A_2 $,$ B_2 $,$ C_2 $,使得$ A_2B_1 = 2A_1B_1 $,$ B_2C_1 = 2B_1C_1 $,$ C_2A_1 = 2C_1A_1 $,顺次连接$ A_2 $,$ B_2 $,$ C_2 $,得到$ △A_2B_2C_2 $,记其面积为$ S_2 $;…,按此规律继续下去,可得到$ △A_5B_5C_5 $,则其面积$ S_5 = $________.

答案:
2476099 提示:在题图中,若连接 $ BC_{1} $,则 $ S_{\triangle BC_{1}A} $ 是 $ S_{\triangle BCA} $ 的 2 倍且 $ S_{\triangle BA_{1}C_{1}} $ 等于 $ S_{\triangle BC_{1}A} $ 的 2 倍,得 $ S_{\triangle AA_{1}C_{1}} $ 是 $ S_{\triangle BCA} $ 的 6 倍;同理连接 $ CA_{1} $,连接 $ AB_{1} $,则 $ S_{\triangle A_{1}BB_{1}} $ 是 $ S_{\triangle BCA} $ 的 6 倍, $ S_{\triangle B_{1}CC_{1}} $ 是 $ S_{\triangle BCA} $ 的 6 倍,则 $ S_{\triangle B_{1}A_{1}C_{1}} $ 等于 19.则第二次操作,总面积是 $ 19^{2} $,到第五次操作,总面积是 $ 19^{5} $,即 2476099.
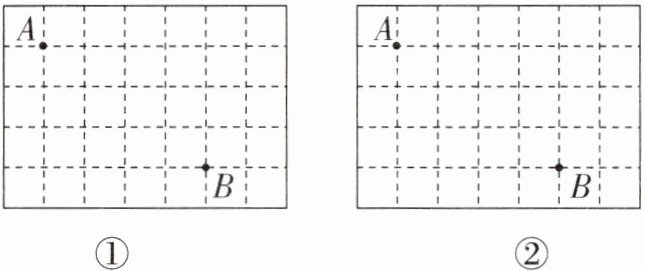
17. (6分)图①、图②是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A,B在小正方形的顶点上.
(1)在图①中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画出一个即可);
(2)在图②中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画出一个即可).
(1)在图①中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画出一个即可);
(2)在图②中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画出一个即可).

答案:
(1)答案不唯一,如图①②,


(2)答案不唯一,如图③④


(1)答案不唯一,如图①②,


(2)答案不唯一,如图③④


18. (6分)如图,△ABC中,AD是BC边上的中线,AE是BC边上的高.
(1)若$ ∠ACB = 100° $,求∠CAE的度数;
(2)若$ S_{△ABC} = 12 $,$ CD = 4 $,求高AE的长.
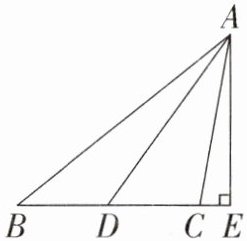
(1)若$ ∠ACB = 100° $,求∠CAE的度数;
(2)若$ S_{△ABC} = 12 $,$ CD = 4 $,求高AE的长.

答案:
(1) $ \because AE $ 是 $ BC $ 边上的高, $ \therefore \angle E = 90^{\circ} $. 又 $ \because \angle ACB = 100^{\circ} $, $ \angle CAE + \angle E = \angle ACB $, $ \therefore \angle CAE = 100^{\circ} - 90^{\circ} = 10^{\circ} $.
(2) $ \because AD $ 是 $ BC $ 上的中线, $ DC = 4 $, $ \therefore D $ 为 $ BC $ 的中点, 且 $ BC = 2DC = 8 $. $ \because AE $ 是 $ BC $ 边上的高, $ S_{\triangle ABC} = 12 $, $ \therefore S_{\triangle ABC} = \frac{1}{2}BC \cdot AE $, 即 $ \frac{1}{2} × 8 × AE = 12 $, $ \therefore AE = 3 $.
(1) $ \because AE $ 是 $ BC $ 边上的高, $ \therefore \angle E = 90^{\circ} $. 又 $ \because \angle ACB = 100^{\circ} $, $ \angle CAE + \angle E = \angle ACB $, $ \therefore \angle CAE = 100^{\circ} - 90^{\circ} = 10^{\circ} $.
(2) $ \because AD $ 是 $ BC $ 上的中线, $ DC = 4 $, $ \therefore D $ 为 $ BC $ 的中点, 且 $ BC = 2DC = 8 $. $ \because AE $ 是 $ BC $ 边上的高, $ S_{\triangle ABC} = 12 $, $ \therefore S_{\triangle ABC} = \frac{1}{2}BC \cdot AE $, 即 $ \frac{1}{2} × 8 × AE = 12 $, $ \therefore AE = 3 $.
查看更多完整答案,请扫码查看


