《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

15. 实数a，b在数轴上的位置如图，化简$|a-b|-\sqrt[3]{a^3}+|ab|+\sqrt{b^2}=$________。

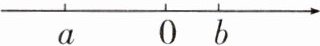
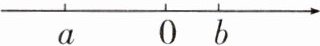
答案： $ 2 b - 2 a - a b $

16. 如图为一个数值转换器。当输入的x值为81时，输出的y值为______；当输入的x值为______后，经过三次取算术平方根运算，输出的y值为$\sqrt{5}$。

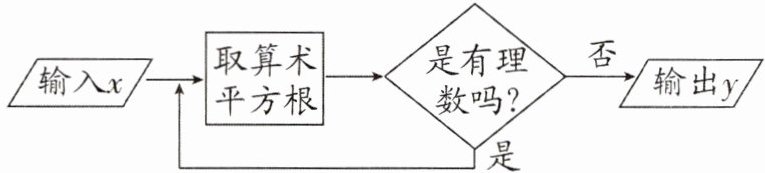
答案： $ \sqrt { 3 } $ 625

17. （8分）计算下面各题：
（1）$|-2|-\sqrt{4}+3^2$；
（2）$(-2)^2-\sqrt[3]{64}-(-3)^0-(\frac{1}{3})^{-2}$；
（3）$-1^4+|1-\sqrt{2}|-(\pi-3.14)^0$；
（4）$20×\sqrt{\frac{4}{25}}-\sqrt[3]{-27}+3÷(-\frac{1}{3})$。

答案：
(1) 9
(2) -10
(3) $ \sqrt { 2 } - 3 $
(4) 2

18. （6分）已知$a+1$的算术平方根是1，-27的立方根是$b-12$，$c-3$的平方根是$\pm2$，求$a+b+c$的平方根。

答案： $ \because a + 1 $ 的算术平方根是 1，$ \therefore a + 1 = 1 $，$ a = 0 $。$ \because - 27 $ 的立方根是 $ b - 12 $，$ \therefore b - 12 = - 3 $，$ b = 9 $。$ \because c - 3 $ 的平方根是 $ \pm 2 $，$ \therefore c - 3 = 4 $，$ c = 7 $。$ \therefore a + b + c = 0 + 9 + 7 = 16 $，$ \therefore a + b + c $ 的平方根是 $ \pm 4 $。

19. （6分）阅读材料：
学习了无理数后，小航用这样的方法估算$\sqrt{6}$的近似值：
由于$\sqrt{4}＜\sqrt{6}＜\sqrt{9}$，不妨设$\sqrt{6}=2+k(0＜k＜1)$，所以$(\sqrt{6})^2=(2+k)^2$，可得$6=4+4k+k^2$。
由$0＜k＜1$可知$0＜k^2＜1$，所以$6\approx4+4k$，解得$k\approx\frac{1}{2}$，则$\sqrt{6}\approx2+\frac{1}{2}\approx2.50$。
依照小航的方法解决下列问题：
（1）估算$\sqrt{13}$的值；
（2）已知非负整数a，b，m，若$a＜\sqrt{m}＜a+1$，且$m=a^2+b$，则$\sqrt{m}\approx$________。（用含a，b的代数式表示）

答案：
(1) 由于 $ \sqrt { 9 } ＜ \sqrt { 13 } ＜ \sqrt { 16 } $，不妨设 $ \sqrt { 13 } = 3 + k ( 0 ＜ k ＜ 1 ) $，所以 $ ( \sqrt { 13 } ) ^ { 2 } = ( 3 + k ) ^ { 2 } $，可得 $ 13 = 9 + 6 k + k ^ { 2 } $，由 $ 0 ＜ k ＜ 1 $，可知 $ 0 ＜ k ^ { 2 } ＜ 1 $，所以 $ 13 \approx 9 + 6 k $，解得 $ k \approx \frac { 2 } { 3 } $，则 $ \sqrt { 13 } \approx 3 + \frac { 2 } { 3 } \approx 3.67 $。
(2) $ a + \frac { b } { 2 a } $