第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
20. (8分)【综合与实践】如图,把两个面积均为$18cm^2$的小正方形纸片分别沿对角线裁剪后拼成一个大的正方形纸片。
(1)大正方形纸片的边长为________cm。
(2)若沿此大正方形纸片边的方向裁剪出一个长方形纸片,能否使裁剪出的长方形纸片的长宽之比为4:3,且面积为$24cm^2$?若能,求剪出的长方形纸片的长和宽;若不能,试说明理由。
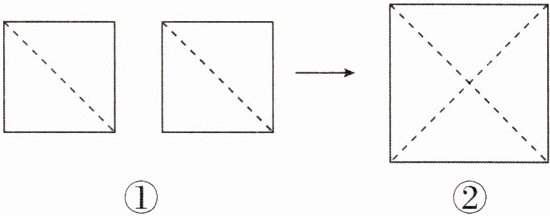
(1)大正方形纸片的边长为________cm。
(2)若沿此大正方形纸片边的方向裁剪出一个长方形纸片,能否使裁剪出的长方形纸片的长宽之比为4:3,且面积为$24cm^2$?若能,求剪出的长方形纸片的长和宽;若不能,试说明理由。

答案:
(1) 6
(2) 沿此大正方形边的方向,能裁剪出符合要求的长方形纸片,理由如下:
$ \because $ 长方形纸片的长宽之比为 $ 4 : 3 $,
$ \therefore $ 设长方形纸片的长和宽分别是 $ 4 x \mathrm { cm } , 3 x \mathrm { cm } $,
$ \therefore 3 x × 4 x = 24 $,$ \therefore x ^ { 2 } = 2 $。
$ \because x > 0 $,$ \therefore x = \sqrt { 2 } $,$ \therefore $ 长方形纸片的长是 $ 4 x = 4 \sqrt { 2 } \mathrm { cm } $。
$ \because 4 \sqrt { 2 } < 6 $,$ \therefore $ 沿此大正方形纸片边的方向,能裁剪出符合要求的长方形纸片。
(1) 6
(2) 沿此大正方形边的方向,能裁剪出符合要求的长方形纸片,理由如下:
$ \because $ 长方形纸片的长宽之比为 $ 4 : 3 $,
$ \therefore $ 设长方形纸片的长和宽分别是 $ 4 x \mathrm { cm } , 3 x \mathrm { cm } $,
$ \therefore 3 x × 4 x = 24 $,$ \therefore x ^ { 2 } = 2 $。
$ \because x > 0 $,$ \therefore x = \sqrt { 2 } $,$ \therefore $ 长方形纸片的长是 $ 4 x = 4 \sqrt { 2 } \mathrm { cm } $。
$ \because 4 \sqrt { 2 } < 6 $,$ \therefore $ 沿此大正方形纸片边的方向,能裁剪出符合要求的长方形纸片。
21. (8分)如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径。
(1)把圆片沿数轴向左滚动半周,点B到达数轴上点C的位置,点C表示的数是________数(填“无理”或“有理”),这个数是________。
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是________。
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,-1,+3,-4,-3。
①第几次滚动后,点A距离原点最近?第几次滚动后,点A距离原点最远?
②当圆片结束运动时,点A运动的路程一共是多少?此时点A所表示的数是多少?
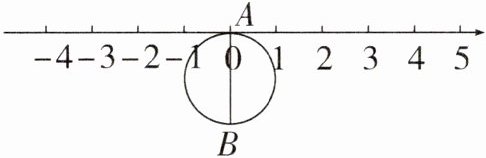
(1)把圆片沿数轴向左滚动半周,点B到达数轴上点C的位置,点C表示的数是________数(填“无理”或“有理”),这个数是________。
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是________。
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,-1,+3,-4,-3。
①第几次滚动后,点A距离原点最近?第几次滚动后,点A距离原点最远?
②当圆片结束运动时,点A运动的路程一共是多少?此时点A所表示的数是多少?

答案:
(1) 无理 $ - \pi $
(2) $ 4 \pi $ 或 $ - 4 \pi $ 或 0
(3) ①第 4 次滚动后,点 A 距离原点最近;第 3 次滚动后,点 A 距离原点最远。
②$ \because | + 2 | + | - 1 | + | + 3 | + | - 4 | + | - 3 | = 13 $,
$ \therefore 13 × 2 \pi × 1 = 26 \pi $,$ \therefore $ 点 A 运动的路程一共是 $ 26 \pi $。
$ \because ( + 2 ) + ( - 1 ) + ( + 3 ) + ( - 4 ) + ( - 3 ) = - 3 $,$ ( - 3 ) × 2 \pi × 1 = - 6 \pi $,$ \therefore $ 此时点 A 所表示的数是 $ - 6 \pi $。
(1) 无理 $ - \pi $
(2) $ 4 \pi $ 或 $ - 4 \pi $ 或 0
(3) ①第 4 次滚动后,点 A 距离原点最近;第 3 次滚动后,点 A 距离原点最远。
②$ \because | + 2 | + | - 1 | + | + 3 | + | - 4 | + | - 3 | = 13 $,
$ \therefore 13 × 2 \pi × 1 = 26 \pi $,$ \therefore $ 点 A 运动的路程一共是 $ 26 \pi $。
$ \because ( + 2 ) + ( - 1 ) + ( + 3 ) + ( - 4 ) + ( - 3 ) = - 3 $,$ ( - 3 ) × 2 \pi × 1 = - 6 \pi $,$ \therefore $ 此时点 A 所表示的数是 $ - 6 \pi $。
查看更多完整答案,请扫码查看


