第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
11. 已知点$M(3,-2)$,将它先向左平移4个单位,再向上平移3个单位后得到点$N$,那么点$N$的坐标是______.
答案:
$(-1,1)$
12. 如果点$P(m,1 + 2m)$在第三象限内,那么$m$的取值范围是______.
答案:
$m<-\frac{1}{2}$
13. 如图,在平面直角坐标系中,$\triangle ABC$的两个顶点$A$,$B$的坐标分别为$(-2,0)$,$(-1,0)$,$BC\perp x$轴. 将$\triangle ABC$以$y$轴为对称轴作对称变换,得到$\triangle A'B'C'(A$和$A'$,$B$和$B'$,$C$和$C'$分别是对应顶点). 直线$y = x + b$经过点$A$,$C'$,则点$C'$的坐标是______.


答案:
$(1,3)$
14. 一个长为120米,宽为100米的矩形场地要扩建成一个正方形场地,设长增加$x$米,宽增加$y$米,则$y$与$x$的函数表达式是______,自变量的取值范围是______,且$y$是$x$的______函数.
答案:
$y=x+20$ $x\geqslant 0$ 一次
15. 在全民健身环城越野赛中,甲、乙两选手的行程$y(\mathrm{km})$随时间$x(\mathrm{h})$变化的图像(全程)如图所示. 有下列说法:①起跑后$1\mathrm{h}$内,甲在乙的前面;②第$1\mathrm{h}$两人都跑了$10\mathrm{km}$;③甲比乙先到达终点;④两人都跑了$20\mathrm{km}$. 其中正确的说法有______个.
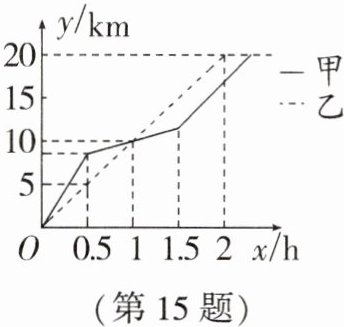

答案:
3
16. 已知直线$y = kx + b$与直线$y = -\frac{2 - x}{3}$平行,且与直线$y = \frac{2x + 1}{3}$交于$y$轴上同一点,则该直线的表达式为______.
答案:
$y=\frac{1}{3}x+\frac{1}{3}$
17. (6分)如图,如果“士”所在的位置坐标为$(-1,-2)$,“相”所在的位置坐标为$(2,-2)$,那么“炮”所在的位置坐标为多少?
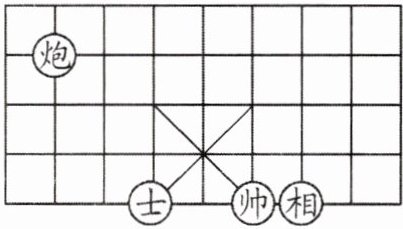

答案:
由“士 ”和“相 ”所在的位置坐标可以确定原点所在的位置在“士"的上 2 格,右 1 格处,从而“炮”所在的位置坐标为$(-3,1)$。
18. (6分)阳光商店在销售某一商品时在进价的基础上加一定利润,其数量$x(\mathrm{kg})$与售价$y$(元)如下表所示,请你根据表中所提供的信息,写出$y$与$x$之间的函数表达式,并求出当数量是$3.5\mathrm{kg}$时的售价是多少元.
| 数量$x/\mathrm{kg}$ | 1 | 2 | 3 | 4 | 5 |
| --- | --- | --- | --- | --- | --- |
| 售价$y/$元 | $8 + 0.4$ | $16 + 0.8$ | $24 + 1.2$ | $32 + 1.6$ | $40 + 2.0$ |
| 数量$x/\mathrm{kg}$ | 1 | 2 | 3 | 4 | 5 |
| --- | --- | --- | --- | --- | --- |
| 售价$y/$元 | $8 + 0.4$ | $16 + 0.8$ | $24 + 1.2$ | $32 + 1.6$ | $40 + 2.0$ |
答案:
由表格提供的信息可知,$y$是$x$的 8 倍加上$x$的 0.4 倍。
$\because y=8x+0.4x=8.4x$,$\therefore y$与$x$之间的函数表达式为$y=8.4x(x\geqslant 0)$。
当$x=3.5$时,$y=8.4× 3.5=29.4$。即当数量是$3.5kg$时的售价是 29.4 元。
$\because y=8x+0.4x=8.4x$,$\therefore y$与$x$之间的函数表达式为$y=8.4x(x\geqslant 0)$。
当$x=3.5$时,$y=8.4× 3.5=29.4$。即当数量是$3.5kg$时的售价是 29.4 元。
查看更多完整答案,请扫码查看


