《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

18. 请把3，-1，4，-2，7，-5这六个数字分别填入正方体的平面展开图的小正方形格内，使它围成正方体后，正方体相对面的数字之和都等于2.

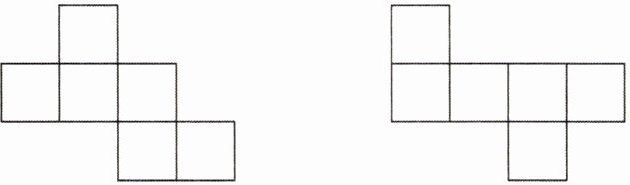
答案：
如图所示(答案不唯一).
　　　　 　　　　

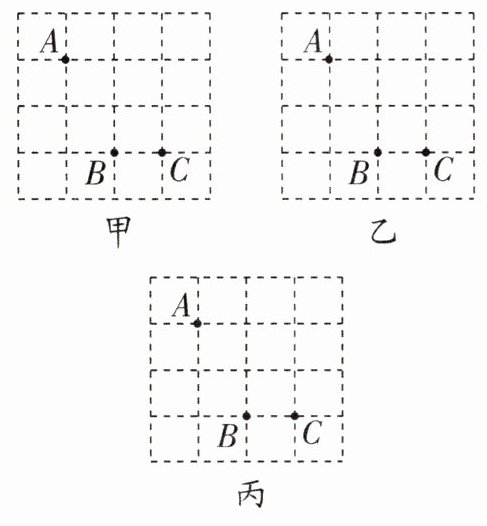
19. 如图，方格纸中有三个点A，B，C，要求作一个四边形使这三个点在这个四边形的边(包括顶点)上，且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形；
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形；
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.

答案：
答案不唯一,例如:
(1)甲图:平行四边形;
(2)乙图:等腰梯形;
(3)丙图:正方形
　　　　　　 　　
　　　　　　　　　

20. 操作示例
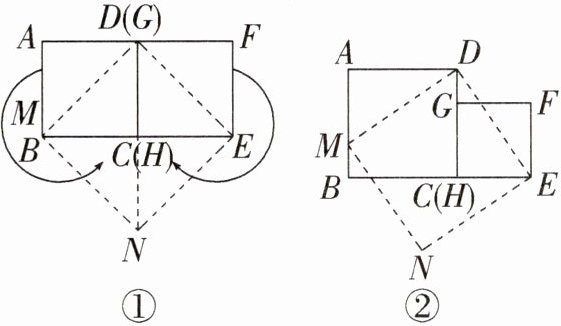
对于边长为a的两个正方形ABCD和EFGH，按图①所示的方式摆放，在沿虚线BD，EG剪开后，可以按图中所示的移动方式拼接为图①中的四边形BNED.
从拼接的过程容易得到结论：
①四边形BNED是正方形；$②S_{正方形ABCD}+S_{正方形EFGH}=S_{正方形BNED}.$实践与探究
(1)对于边长分别为a，b(a＞b)的两个正方形ABCD和EFGH，按图②所示的方式摆放，连接DE，过点D作DM⊥DE，交AB于点M，过点M作MN⊥DM，过点E作EN⊥DE，MN与EN相交于点N.
①证明四边形MNED是正方形，并用含a，b的代数式表示正方形MNED的面积；
②在图中，将正方形ABCD和正方形EFGH沿虚线剪开后，能够拼接为正方形MNED，请简要说明你的拼接方法(类比图①，用数字表示对应的图形).
(2)对于n(n是大于2的自然数)个任意的正方形，能否通过若干次拼接，将其拼接成为一个正方形？请简要说明你的理由.

答案：

(1)①由作图的过程可知四边形MNED是矩形。
在Rt△ADM与Rt△CDE中,
∵AD=CD,又∠ADM+∠MDC=∠CDE+∠MDC=90°,
∴∠ADM=∠CDE,
∴Rt△ADM≌Rt△CDE,
∴DM=DE,
∴四边形MNED是正方形。
∵DE²=CD²+CE²=a²+b²,
∴正方形MNED的面积为a² + b²。
②过点N作NP⊥BE,垂足为P,如图可以证明图中6与5位置的两个三角形全等，4与3位置的两个三角形全等，2与1位置的两个三角形也全等。所以将6 放到5的位置，4放到3的位置,2放到1的位置，恰好拼接为正方形MNED。
　　　　　　　　
(2)能。理由是:由上述的拼接过程可以看出:对于任意的两个正方形都可以拼接为一个正方形，而拼接出的这个正方形可以与第三个正方形再拼接为一个正方形……依次类推,由此可知:对于n个任意的正方形，可以通过若干次拼接，得到一个正方形。