《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

14. 三角形三边长分别为4,$a$,7,那么$a$的取值范围是____.

答案： $ 3 ＜ a ＜ 11 $

15. 一水果商店某次按每千克3.2元购进一批苹果,销售过程中有20%的苹果正常损耗,为避免亏本,该水果商店应将这批苹果的售价至少定为每千克____元.

答案： 4

16. 按下图所示的程序进行运算:
并规定:程序运行到“结果是否大于65”为一次运算,且运算进行4次才停止,则可输入的整数$x$的个数是____.

答案： 4

17. (6分)(1)解不等式$3(x - 1)＞2x + 2$;
(2)解不等式$\frac{2x - 1}{3}-\frac{9x + 2}{6}\leqslant1$,并把解集表示在数轴上.

答案：

(1) $ x ＞ 5 $
(2) $ x \geq - 2 $，如图：

18. (6分)(1)解不等式组$\begin{cases}3x＞x - 2,\frac{x + 1}{3}＞2x;\end{cases}$
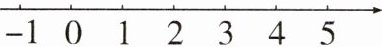
(2)解不等式组$\begin{cases}3(x + 2)＞x + 8,\frac{x}{4}\geqslant\frac{x - 1}{3},\end{cases}$并把它的解集在如图所示的数轴上表示出来.

答案：
(1) $ - 1 ＜ x ＜ \frac{1}{5} $
(2) $ 1 ＜ x \leq 4 $ 图略

19. (6分)已知不等式$\frac{1}{3}(x - m)＞2 - m$.
(1)若其解集为$x＞3$,求$m$的值;
(2)若满足$x＞3$的每一个数都能使已知不等式成立,求$m$的取值范围.

答案：
(1) 不等式整理得 $ x - m ＞ 6 - 3m $，解得 $ x ＞ 6 - 2m $，
由不等式的解集为 $ x ＞ 3 $，得到 $ 6 - 2m = 3 $，解得 $ m = 1.5 $。
(2) 由满足 $ x ＞ 3 $ 的每一个数都能使已知不等式成立，
得到 $ 6 - 2m \leq 3 $，解得 $ m \geq 1.5 $。