《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

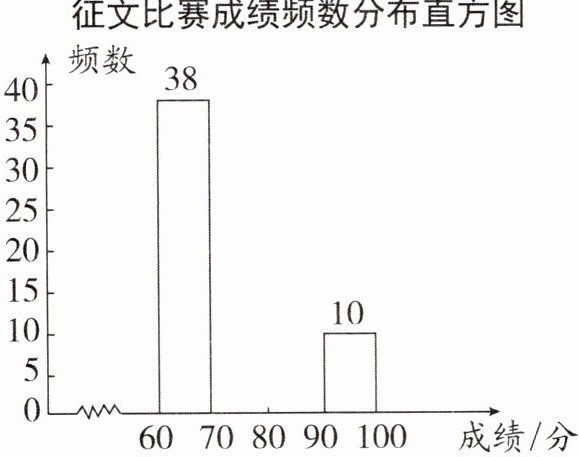
19. （9分）某市举行“传承好家风”征文比赛，已知每篇参赛征文成绩记$m$分（$60\leq m\leq100$），组委会从1000篇征文中随机抽取了部分参赛征文，统计了它们的成绩，并绘制了如下不完整的两幅统计图表.
请根据以上信息，解决下列问题：
（1）征文比赛成绩频数分布表中$c$的值是_______；
（2）补全征文比赛成绩频数分布直方图；
（3）若80分以上（含80分）的征文将被评为一等奖，试估计全市获得一等奖征文的篇数.

答案：
(1)0.2
(2)由 $60 \leq m ＜ 70$ 分数段可知，共抽取了 $38 ÷ 0.38 = 100$ (篇)参赛征文， $ \therefore a = 100 × 0.32 = 32$， $b = 100 - (38 + 32 + 10) = 20$。
频数分布直方图略。
(3) $1000 × (0.2 + 0.1) = 300$ (篇)。
答：估计全市获得一等奖征文的有 300 篇。

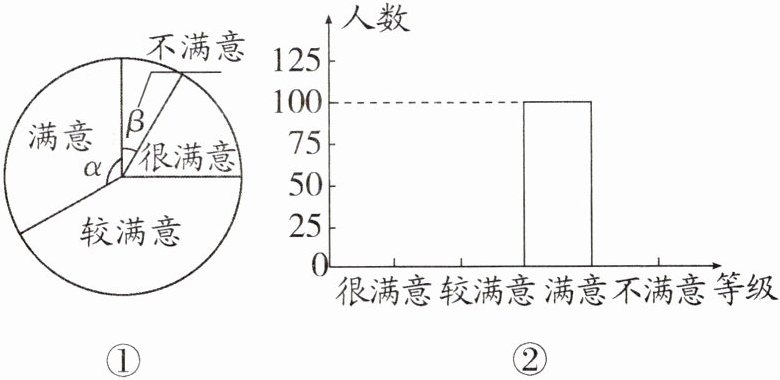
20. （9分）某单位认真开展学习和实践活动，在阶段总结中提出对本单位今后的整改措施，并在征求职工对整改方案的满意程度时进行民主测评，测评等级为很满意、较满意、满意、不满意四个等级.
（1）若测评后结果如扇形统计图（图①），且测试等级为很满意、较满意、满意、不满意的人数之比为2:5:4:1，则图中$\alpha=$______，$\beta=$______；
（2）若测试后部分统计结果如直方图（图②），请将直方图补画完整，并求出该单位职工总人数；
（3）按上级要求，满意度必须不少于95%方案才能通过，否则，必须对方案进行完善.若要使该方案完善后能获得通过，至少还需增加多少人对该方案完善后的测评等级达到满意（含满意）以上？

答案：

(1) $120^{\circ}$ $30^{\circ}$
(2)观察题中统计图知满意的有 100 人。故总人数为 $100 ÷ \frac{4}{2 + 5 + 4 + 1} = 300$ (人)。很满意的有 $300 × \frac{2}{12} = 50$ (人)；较满意的有 $300 × \frac{5}{12} = 125$ (人)；不满意的有 $300 × \frac{1}{12} = 25$ (人)。
补全直方图如图所示

(3)设至少还需增加 $x$ 人对该方案的测评等级达到满意(含满意)以上。根据题意，得 $ \frac{x + 125 + 50 + 100}{300} = 95\%$，解得 $x = 10$。
故至少还需增加 10 人对该方案的测评等级达到满意(含满意)以上。