《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

8. 如图，在直角坐标系中，以原点 $ O $ 为圆心的同心圆的半径，由内向外依次为 1，2，3，4，$ \cdots $，同心圆与直线 $ y = x $ 和 $ y = - x $ 分别交于 $ A _ { 1 } $，$ A _ { 2 } $，$ A _ { 3 } $，$ A _ { 4 } $，$ \cdots $，则点 $ A _ { 30 } $ 的坐标是（ ）

A.$ ( 30,30 ) $
B.$ ( - 8 \sqrt { 2 }, 8 \sqrt { 2 } ) $
C.$ ( - 4 \sqrt { 2 }, 4 \sqrt { 2 } ) $
D.$ ( 4 \sqrt { 2 }, - 4 \sqrt { 2 } ) $

答案： C

9. 有一列数：$ - \frac { 1 } { 2 } $，$ \frac { 2 } { 5 } $，$ - \frac { 3 } { 10 } $，$ \frac { 4 } { 17 } $，$ \cdots $，那么第 7 个数是________。

答案： $-\frac{7}{50}$

10. 规定运算：$ a ☆ b = \sqrt { a } - \sqrt { b } $，$ a ※ b = \sqrt { a } + \sqrt { b } $，其中 $ a $，$ b $ 为实数，则 $ ( 3 ☆ 5 ) ( 3 ※ 5 ) = $________。

答案： −2

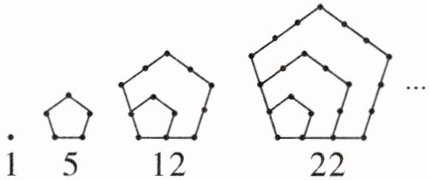
11. 古希腊人常用小石子在沙滩上摆成各种形状来研究数。例如：
称图中的数 1，5，12，22，$ \cdots $ 为五边形数，则第 6 个五边形数是________。

答案： 51

12. 设 $ a _ { 1 } $，$ a _ { 2 } $，$ \cdots $，$ a _ { 27 } $ 是从 1，0，$ - 1 $ 这三个数中取值的一列数，若 $ a _ { 1 } + a _ { 2 } + \cdots + a _ { 27 } = 10 $，$ ( a _ { 1 } + 1 ) ^ { 2 } + ( a _ { 2 } + 1 ) ^ { 2 } + \cdots + ( a _ { 27 } + 1 ) ^ { 2 } = 67 $，则 $ a _ { 1 } $，$ a _ { 2 } $，$ \cdots $，$ a _ { 27 } $ 中 0 的个数为________。

答案： 7

13. 在如图所示的平面直角坐标系中，$ \triangle O A _ { 1 } B _ { 1 } $ 是边长为 2 的等边三角形，作 $ \triangle B _ { 2 } A _ { 2 } B _ { 1 } $ 与 $ \triangle O A _ { 1 } B _ { 1 } $ 关于点 $ B _ { 1 } $ 成中心对称，再作 $ \triangle B _ { 2 } A _ { 3 } B _ { 3 } $ 与 $ \triangle B _ { 2 } A _ { 2 } B _ { 1 } $ 关于点 $ B _ { 2 } $ 成中心对称，如此作下去，则 $ \triangle B _ { 2 n } A _ { 2 n + 1 } B _ { 2 n + 1 } $（$ n $ 是正整数）的顶点 $ A _ { 2 n + 1 } $ 的坐标是________。

答案： (4n+1,√3)

14. 任意大于 1 的正整数 $ m $ 的三次幂均可“分裂”成 $ m $ 个连续奇数的和，如：$ 2 ^ { 3 } = 3 + 5 $，$ 3 ^ { 3 } = 7 + 9 + 11 $，$ 4 ^ { 3 } = 13 + 15 + 17 + 19 $，$ \cdots $，按此规律，若 $ m ^ { 3 } $ 分裂后其中有一个奇数是 121，则 $ m $ 的值是________。

答案： 11

15. 读一读：式子“$ 1 + 2 + 3 + 4 + \cdots + 100 $”表示从 1 开始的 100 个连续自然数的和，由于式子比较长，书写不方便，为了简便起见，我们将其表示为 $ \sum _ { n = 1 } ^ { 100 } n $，这里“$ \sum $”是求和符号。通过对以上材料的阅读，请计算：$ \sum _ { n = 1 } ^ { 999 } \frac { 1 } { n ( n + 1 ) } = $________。

答案： $\frac{999}{1000}$

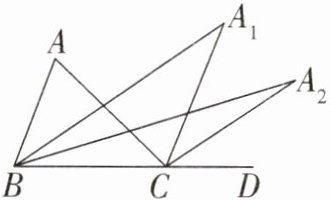
16. 如图，$ \angle A C D $ 是 $ \triangle A B C $ 的外角，$ \angle A B C $ 的平分线与 $ \angle A C D $ 的平分线交于点 $ A _ { 1 } $，$ \angle A _ { 1 } B C $ 的平分线与 $ \angle A _ { 1 } C D $ 的平分线交于点 $ A _ { 2 } $，$ \cdots $，$ \angle A _ { n - 1 } B C $ 的平分线与 $ \angle A _ { n - 1 } C D $ 的平分线交于点 $ A _ { n } $，设 $ \angle A = \theta $，则：（1）$ \angle A _ { 1 } = $________；（2）$ \angle A _ { n } = $________。

答案：
(1)$\frac{\theta}{2}$　
(2)$\frac{\theta}{2^n}$