《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

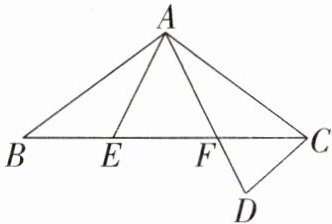
18. （6分）如图，$△ABC$中，$AB=AC$，点E，F在边BC上，$BE=CF$，点D在AF的延长线上，$AD=AC$。
（1）求证：$△ABE\cong △ACF$；
（2）若$∠BAE=30^{\circ }$，则$∠ADC=$______$^{\circ }$。

答案：
(1) $ \because AB = AC$，$ \therefore \angle B = \angle ACF$。
在 $ \triangle ABE $ 和 $ \triangle ACF $ 中，$ \left\{ \begin{array} { l } { AB = AC, } \\ { \angle B = \angle ACF, } \\ { BE = CF, } \end{array} \right. $
$ \therefore \triangle ABE \cong \triangle ACF(SAS)$。
(2) 75 提示：$ \because \triangle ABE \cong \triangle ACF$，$ \angle BAE = 30^\circ$，$ \therefore \angle BAE = \angle CAF = 30^\circ$。$ \because AD = AC$，$ \therefore \angle ADC = \angle ACD = \frac { 180 ^ { \circ } - 30 ^ { \circ } } { 2 } = 75 ^ { \circ }$。

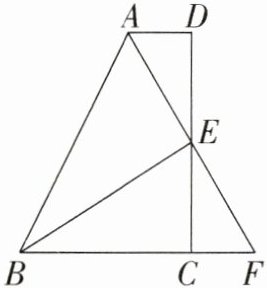
19. （8分）如图所示，在四边形ABCD中，$AD// BC$，E为CD的中点，连接AE，BE，延长AE交BC的延长线于点F。
（1）判断FC与AD的数量关系，并说明理由；
（2）若$AB=BC+AD$，则$BE⊥AF$吗？为什么？

答案：
(1) $ FC = AD$。理由：$ \because AD // BC$，$ \therefore \angle ADC = \angle ECF$。$ \because E $ 是 $ CD $ 的中点，$ \therefore DE = EC$。在 $ \triangle ADE $ 与 $ \triangle FCE $ 中，$ \left\{ \begin{array} { l } { \angle ADE = \angle ECF, } \\ { ED = EC, } \\ { \angle AED = \angle CEF, } \end{array} \right. $
$ \therefore \triangle ADE \cong \triangle FCE(ASA)$，$ \therefore FC = AD$。
(2) $ BE \perp AF$。理由：由
(1) 知 $ \triangle ADE \cong \triangle FCE$，$ \therefore AE = EF$，$ AD = CF$。$ \because AB = BC + AD$，$ \therefore AB = BC + CF$，即 $ AB = BF$。$ \therefore BE \perp AF$。

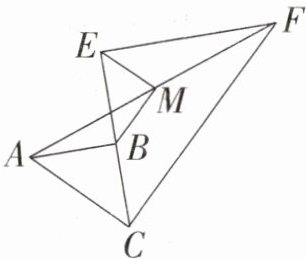
20. （8分）已知两个共顶点的等腰$Rt△ABC$和等腰$Rt△CEF$，$∠ABC=∠CEF=90^{\circ }$，连接AF，M是AF的中点，连接MB，ME。
（1）如图，当CB与CE在同一条直线上时，求证：$BM// CF$；
（2）在（1）中，若$AB=a$，$CE=2a$，求BM，ME的长。

答案：
(1) 连接 $ CM$。由题知 $ AB = BC$，$ BM = BM$，$ \angle ACB = 45 ^ { \circ }$，$ \angle ECF = 45 ^ { \circ }$，$ \therefore \angle ACF = 90 ^ { \circ }$，$ \therefore CM = \frac { 1 } { 2 } AF = AM$，$ \therefore \triangle ABM \cong \triangle CBM$，$ \therefore \angle CMB = \angle AMB$，$ \therefore BM \perp AC$。又 $ AC \perp CF$，$ \therefore BM // CF$。
(2) 由
(1) 知 $ CM = AM = FM$，又 $ EC = EF$，$ EM = EM$，$ \therefore \triangle ECM \cong \triangle EFM$。
$ \therefore \angle CEM = \angle FEM = \frac { 1 } { 2 } \angle CEF = 45 ^ { \circ }$，$ \therefore EM \perp CF$。
又 $ BM // CF$，$ \therefore EM \perp BM$，
$ \therefore \angle EMB = 90 ^ { \circ }$，$ \therefore \triangle EMB $ 是等腰直角三角形。
$ \because AB = a$，$ CE = 2 a$，$ \therefore BC = BE = a$。
$ \therefore ME = BM = \frac { \sqrt { 2 } } { 2 } a$。

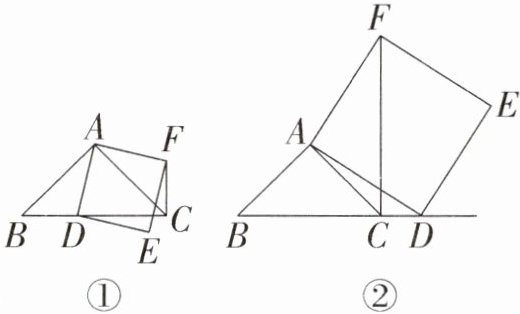
21. （8分）如图①，在$△ABC$中，$∠ACB$为锐角。点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF。如果$AB=AC$，$∠BAC=90^{\circ }$。
解答下列问题：
（1）当点D在线段BC上时（与点B不重合），如图①，线段CF，BD之间的位置关系为______，数量关系为______；
（2）当点D在线段BC的延长线上时，如图②，（1）中的结论是否仍然成立，为什么？（要求写出证明过程）

答案：
(1) 垂直　相等　提示：$ \because $ 四边形 $ ADEF $ 是正方形，$ \therefore \angle DAF = 90 ^ { \circ }$，$ AD = AF$。$ \because AB = AC$，$ \angle BAC = 90 ^ { \circ }$，
$ \therefore \angle BAD + \angle DAC = \angle CAF + \angle DAC = 90 ^ { \circ }$，
$ \therefore \angle BAD = \angle CAF$。
在 $ \triangle BAD $ 和 $ \triangle CAF $ 中，$ \left\{ \begin{array} { l } { AB = AC, } \\ { \angle BAD = \angle CAF, } \\ { AD = AF, } \end{array} \right. $
$ \therefore \triangle BAD \cong \triangle CAF(SAS)$，$ \therefore CF = BD$，$ \therefore \angle B = \angle ACF$。$ \because \angle B + \angle BCA = 90 ^ { \circ }$，$ \therefore \angle BCA + \angle ACF = 90 ^ { \circ }$，即 $ CF \perp BD$。
(2) 当点 $ D $ 在 $ BC $ 的延长线上时，① 中的结论仍成立。
理由：$ \because $ 四边形 $ ADEF $ 是正方形，$ \therefore \angle DAF = 90 ^ { \circ }$，$ AD = AF$。$ \because AB = AC$，$ \angle BAC = 90 ^ { \circ }$，$ \therefore \angle BAD - \angle DAC = \angle CAF - \angle DAC = 90 ^ { \circ }$，$ \therefore \angle BAD = \angle CAF$。
在 $ \triangle BAD $ 和 $ \triangle CAF $ 中，$ \left\{ \begin{array} { l } { AB = AC, } \\ { \angle BAD = \angle CAF, } \\ { AD = AF, } \end{array} \right. $
$ \therefore \triangle BAD \cong \triangle CAF(SAS)$，$ \therefore CF = BD$，$ \therefore \angle B = \angle ACF$。$ \because \angle B + \angle BCA = 90 ^ { \circ }$，$ \therefore \angle BCA + \angle ACF = 90 ^ { \circ }$，即 $ CF \perp BD$。