《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

19. （6分）已知点$Q$与$P(2,3)$关于$x$轴对称，一个一次函数的图像经过点$Q$，且与$y$轴的交点$M$与原点的距离为5，求这个一次函数的表达式.

答案： $\because Q$与$P(2,3)$关于$x$轴对称，$\therefore$点$Q$的坐标为$(2,-3)$。
设一次函数的表达式为$y=kx+b(k\neq 0)$。
$\because$函数与$y$轴的交点$M$与原点的距离为 5，$\therefore b=\pm 5$。
又函数的图像经过点$Q$，$\therefore 2k+b=-3$。当$b=5$时，$2k+5=-3$，解得$k=-4$；当$b=-5$时，$2k-5=-3$，解得$k=1$。
故一次函数的表达式为$y=-4x+5$或$y=x-5$。

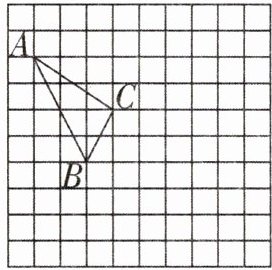
20. （6分）在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）$ABC$的顶点$A$，$C$的坐标分别为$(-4,5)$，$(-1,3)$.
（1）请在如图所示的网格平面内作出平面直角坐标系；
（2）请作出$\triangle ABC$关于$y$轴对称的$\triangle A'B'C'$；
（3）点$B'$的坐标为______；
（4）$\triangle ABC$的面积为______.

答案：

(1)
(2)如图：
　　　　　　
(3)$(2,1)$
(4)4 提示：$S_{\triangle ABC}=3× 4-\frac{1}{2}× 2× 3-\frac{1}{2}× 1× 2-\frac{1}{2}× 2× 4=12-3-1-4=4$。

21. （6分）某工厂计划生产甲、乙两种产品共2500吨，每生产1吨甲产品可获得利润0.3万元，每生产1吨乙产品可获得利润0.4万元. 设该工厂生产了甲产品$x$（吨），生产甲、乙两种产品获得的总利润为$y$（万元）.
（1）求$y$与$x$之间的函数表达式；
（2）若每生产1吨甲产品需要$A$原料0.25吨，每生产1吨乙产品需要$A$原料0.5吨. 受市场影响，该厂能获得的$A$原料至多为1000吨，其他原料充足，求出该工厂生产甲、乙两种产品各为多少吨时，能获得最大利润.

答案：
(1)$y=x× 0.3+(2500-x)× 0.4=-0.1x+1000(0\leqslant x\leqslant 2500)$。
(2)由题意得$x× 0.25+(2500-x)× 0.5\leqslant 1000$，解得$x\geqslant 1000$。
因为$y$的值随着$x$的增大而减小，所以当$x=1000$时，$y$取最大值，$2500-x=1500$。
答：该工厂生产甲种产品 1000 吨，乙种产品 1500 吨时，能获得最大利润。

22. （6分）已知直线$y = kx + b(k\neq 0)$过点$(1,2)$.
（1）填空：$b =$______（用含$k$的代数式表示）；
（2）将此直线向下平移2个单位长度，设平移后的直线交$x$轴于点$A$，交$y$轴于点$B$，$x$轴上另有点$C(1 + k,0)$，使得$\triangle ABC$的面积为2，求$k$的值；
（3）当$1\leqslant x\leqslant 3$时，函数值$y$总大于零，求$k$的取值范围.

答案：
(1)$2 - k$
(2)由
(1)可得$y=kx+2 - k$，
将直线向下平移 2 个单位长度所得直线的表达式为$y=kx - k$，易得$A(1,0)$，$B(0,-k)$，$C(1 + k,0)$，$\therefore AC=\vert 1 + k - 1\vert=\vert k\vert$。
$\therefore S_{\triangle ABC}=\frac{1}{2}AC\cdot \vert y_{B}\vert=\frac{1}{2}\vert k\vert\cdot \vert - k\vert=\frac{1}{2}k^{2}=2$，解得$k=\pm 2$。
(3)当自变量$x$在$1\leqslant x\leqslant 3$变化时，函数值$y$的最小值大于 0。
分两种情况：①当$k＞0$时，$y$随$x$增大而增大，$\therefore$当$x=1$时，$y$有最小值，最小值为$k + 2 - k=2＞0$，$\therefore$当$k＞0$时，函数值总大于 0；
②当$k＜0$时，$y$随$x$增大而减小，$\therefore$当$x=3$时，$y$有最小值，最小值为$3k + 2 - k=2k + 2$，由$2k + 2＞0$得$k＞-1$，$\therefore - 1＜k＜0$。
综上所述，当$k＞0$或$-1＜k＜0$时，函数值$y$总大于 0。