《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

18. （6分）如图是一个4×4的正方形网格，每个小正方形的边长为1。请你在网格中以左上角的三角形为基本图形，通过平移、对称或旋转变换，设计一个精美图案，使其满足：①既是轴对称图形，又是以点O为对称中心的中心对称图形；②所作图案用阴影标识，且阴影部分面积为4。

答案：
题中所给左上角的三角形的面积为 $\frac{1}{2}×1×1=\frac{1}{2}$，故设计图案总共需要三角形 $4÷\frac{1}{2}=8$ (个)，以点 $O$ 为对称中心的中心对称图形，同时又是轴对称图形的设计方案不唯一，如图所示的几种：
　　　

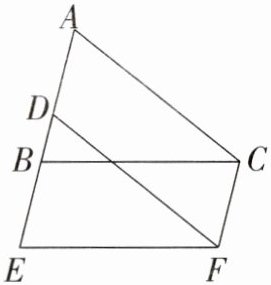
19. （6分）如图，将△ABC沿射线AB的方向平移2个单位到△DEF的位置，点A，B，C的对应点分别为点D，E，F。
(1)直接写出图中与AD相等的线段；
(2)若AB=3，则AE=______；
(3)若∠ABC=75°，求∠CFE的度数。

答案：
(1)与 $AD$ 相等的线段有 $BE$，$CF$.
(2)5 提示：$\because AB = 3$，将 $\triangle ABC$ 沿射线 $AB$ 的方向平移 2 个单位到 $\triangle DEF$ 的位置，$\therefore BE = 2$，则 $AE = BE + AB = 5$. 故答案为 5.
(3)由平移变换的性质得：$BC// EF$，$AE// CF$，$\therefore ∠E = ∠ABC = 75^{\circ}$，$∠CFE + ∠E = 180^{\circ}$，$\therefore ∠CFE = 105^{\circ}$.