《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

20. (8分)如图,在方格纸中(小正方形的边长为1),反比例函数$ y = \frac{k}{x} $的图像与直线的交点A,B均在格点上,根据所给的平面直角坐标系(O是坐标原点),解答下面的问题:
(1)分别写出点A,B的坐标后,把直线AB向右平移5个单位长度,再向上平移5个单位长度,画出平移后的直线$ A'B' $;
(2)若点C在函数$ y = \frac{k}{x} $的图像上,$ \triangle ABC $是以AB为底的等腰三角形,请直接写出点C的坐标.

答案：

(1) $A(-1,-4)$，$B(-4,-1)$. 平移后的直线 $A'B'$ 如图所示
(2) 如图，点 $C$ 的坐标为 $(-2,-2)$ 或 $(2,2)$.

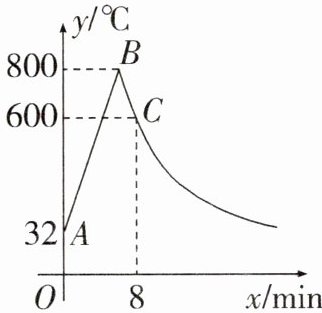
21. (8分)工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料煅烧到$ 800^{\circ}C $,然后停止煅烧进行锻造操作.第8min时,材料温度降为$ 600^{\circ}C $,煅烧时,温度$ y(^{\circ}C) $与时间$ x(min) $成一次函数关系;锻造时,温度$ y(^{\circ}C) $与时间$ x(min) $成反比例关系(如图),已知该材料初始温度是$ 32^{\circ}C $.
(1)分别求出材料煅烧和锻造时y与x的函数表达式,并且写出自变量x的取值范围.
(2)根据工艺要求,当材料温度低于$ 480^{\circ}C $时,需停止操作,那么锻造的操作时间有多长?

答案：
(1) 设锻造时的函数表达式为 $y = \frac{k}{x}$，则 $600 = \frac{k}{8}$，
∴ $k = 4800$.
∵ 该材料初始温度为 $32^{\circ}C$，煅烧到 $800^{\circ}C$ 停止加热，所以 $y$ 的取值范围为 $32 \leq x \leq 800$.
当 $y = 32$ 时，$x = 150$；当 $y = 800$ 时，$x = 6$，
∴ $6 \leq x \leq 150$.
∴ 锻造时的函数表达式为 $y = \frac{4800}{x}(6 \leq x \leq 150)$.
设煅烧时的函数表达式为 $y = kx + b$，则 $\begin{cases} b = 32, \\ 6k + b = 800, \end{cases}$ 解得 $\begin{cases} k = 128, \\ b = 32, \end{cases}$
∴ 煅烧时的函数表达式为 $y = 128x + 32(0 \leq x \leq 6)$.
(2) 当 $y = 480$ 时，$x = \frac{4800}{480} = 10$，$10 - 6 = 4$，
∴ 锻造的操作时间有 $4$ min.