第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
20. (6分)若不等式组$\begin{cases}2x - a<1,\\x - 2b>3\end{cases}$的解集为$-1<x<1$,求$(a + 1)(b - 1)$的值.
答案:
由原不等式组得 $ \begin{cases} x < \frac{1}{2}(a + 1) \\ x > 2b + 3 \end{cases} $。
∵ 该不等式组的解集为 $ - 1 < x < 1 $,
∴ $ \begin{cases} \frac{1}{2}(a + 1) = 1 \\ 2b + 3 = - 1 \end{cases} $。
解得 $ \begin{cases} a = 1 \\ b = - 2 \end{cases} $,
∴ $ (a + 1)(b - 1) = 2 × (- 3) = - 6 $。
∵ 该不等式组的解集为 $ - 1 < x < 1 $,
∴ $ \begin{cases} \frac{1}{2}(a + 1) = 1 \\ 2b + 3 = - 1 \end{cases} $。
解得 $ \begin{cases} a = 1 \\ b = - 2 \end{cases} $,
∴ $ (a + 1)(b - 1) = 2 × (- 3) = - 6 $。
21. (6分)关于$x$的不等式组$\begin{cases}\frac{x + 15}{2}>x - 3,\frac{2x + 2}{3}<x + a\end{cases}$只有4个整数解.
(1)求$a$的取值范围;
(2)当$a$取最大值时,在数轴上表示不等式组的解集.
(1)求$a$的取值范围;
(2)当$a$取最大值时,在数轴上表示不等式组的解集.
答案:
(1) $ - 5 < a \leq - \frac{14}{3} $。
(2) 当 $ a $ 取最大值,即 $ a = - \frac{14}{3} $ 时,
不等式组的解集为 $ 16 < x < 21 $,
其解集在数轴上表示如下。
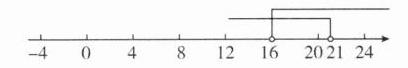
(1) $ - 5 < a \leq - \frac{14}{3} $。
(2) 当 $ a $ 取最大值,即 $ a = - \frac{14}{3} $ 时,
不等式组的解集为 $ 16 < x < 21 $,
其解集在数轴上表示如下。
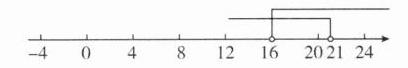
22. (6分)已知甲、乙两种原料中均含有$A$元素,其含量及每吨原料的购买单价如下表所示:
| |$A$元素含量|单价/(万元/t)|
|--|--|--|
|甲原料|5%|2.5|
|乙原料|8%|6|
已知用甲原料提取每千克$A$元素要排放废气1t,用乙原料提取每千克$A$元素要排放废气0.5t.若某厂要提取$A$元素20kg,并要求废气排放不超过16t,问:该厂购买这两种原料最少需要多少万元?
| |$A$元素含量|单价/(万元/t)|
|--|--|--|
|甲原料|5%|2.5|
|乙原料|8%|6|
已知用甲原料提取每千克$A$元素要排放废气1t,用乙原料提取每千克$A$元素要排放废气0.5t.若某厂要提取$A$元素20kg,并要求废气排放不超过16t,问:该厂购买这两种原料最少需要多少万元?
答案:
设购买甲、乙两种原料分别为 $ x $ t 和 $ y $ t,则
$ \begin{cases} 5\% \cdot x \cdot 1000 + 8\% \cdot y \cdot 1000 = 20 \\ 5\% \cdot x \cdot 1000 × 1 + 8\% \cdot y \cdot 1000 × 0.5 \leq 16 \end{cases} $,
即 $ \begin{cases} 5x + 8y = 2 \\ 50x + 40y \leq 16 \end{cases} $,
∴ $ y \geq 0.1 $。
设购买甲、乙两种原料所需要的费用为 $ W $ 万元,则
$ W = 2.5x + 6y = 2.5 × \frac{2 - 8y}{5} + 6y = 1 + 2y \geq 1.2 $,
∴ 当 $ y = 0.1 $,$ x = 0.24 $ 时,$ W_{\text{最小}} = 1.2 $。
故该厂购买这两种原料最少需要 1.2 万元。
$ \begin{cases} 5\% \cdot x \cdot 1000 + 8\% \cdot y \cdot 1000 = 20 \\ 5\% \cdot x \cdot 1000 × 1 + 8\% \cdot y \cdot 1000 × 0.5 \leq 16 \end{cases} $,
即 $ \begin{cases} 5x + 8y = 2 \\ 50x + 40y \leq 16 \end{cases} $,
∴ $ y \geq 0.1 $。
设购买甲、乙两种原料所需要的费用为 $ W $ 万元,则
$ W = 2.5x + 6y = 2.5 × \frac{2 - 8y}{5} + 6y = 1 + 2y \geq 1.2 $,
∴ 当 $ y = 0.1 $,$ x = 0.24 $ 时,$ W_{\text{最小}} = 1.2 $。
故该厂购买这两种原料最少需要 1.2 万元。
查看更多完整答案,请扫码查看


