《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

11. 如图，在菱形 $ABCD$ 中，若 $\angle ABC = 120^{\circ}$，则 $BD:AC =$________。

答案： $1:\sqrt{3}$

12. 如图，在 $\triangle ABC$ 中，$AD$，$CD$ 分别平分 $\angle BAC$ 和 $\angle ACB$，$AE // CD$，$CE // AD$。若从三个条件：①$AB = AC$；②$AB = BC$；③$AC = BC$ 中，选择一个作为已知条件，则能使四边形 $ADCE$ 为菱形的是________（填序号）。

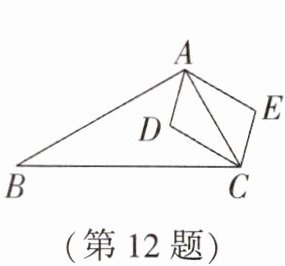
答案： ②

13. 如图，在正方形 $ABCD$ 中，点 $F$ 为 $CD$ 上一点，$BF$ 与 $AC$ 交于点 $E$，若 $\angle CBF = 20^{\circ}$，则 $\angle DEF =$________。

答案： $50^{\circ}$

14. 如图，长方形 $ABCD$ 沿 $EF$ 折叠，使点 $B$，$C$ 分别落在 $D_1$，$C_1$ 位置，若 $\angle CFC_1 = 130^{\circ}$，则 $\angle AED_1$ 等于________。

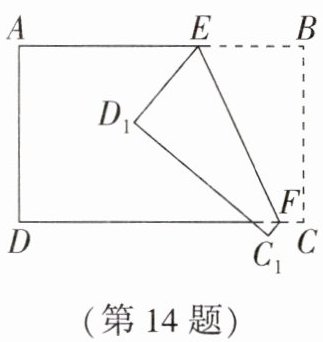
答案： $50^{\circ}$

15. 如图，正方形 $ABCD$ 的边长为 $4$，点 $P$ 在 $DC$ 边上且 $DP = 1$，点 $Q$ 是 $AC$ 上一动点，则 $DQ + PQ$ 的最小值为________。

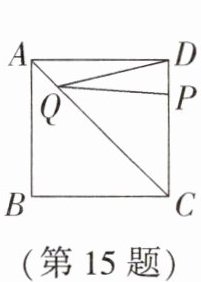
答案： 5

16. 如图，$E$，$F$，$G$，$H$ 分别是任意四边形 $ABCD$ 中 $AD$，$BD$，$BC$，$CA$ 的中点，当四边形 $ABCD$ 的边至少满足________时，四边形 $EFGH$ 是菱形。

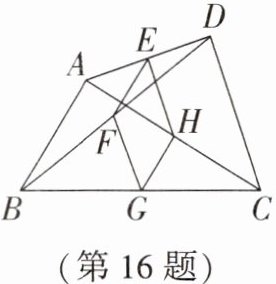
答案： $AB = CD$

17. （6 分）如图，在矩形 $ABCD$ 中，点 $E$ 是 $BC$ 上一点，$AE = AD$，$DF \perp AE$，垂足为 $F$。求证：$DF = DC$。

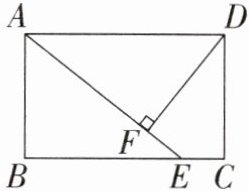
答案： $ \because $ 四边形 $ ABCD $ 是矩形，$ \therefore AD // BC $，$ \therefore \angle DAF = \angle BEA $。又 $ DF \perp AE $，$ \therefore \angle DFA = 90^{\circ} = \angle B $。又 $ AD = AE $，$ \therefore \triangle ABE \cong \triangle DFA $，$ \therefore DF = AB $。又 $ AB = DC $，$ \therefore DF = DC $。

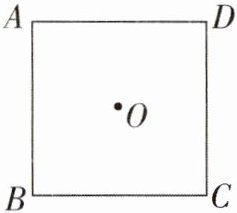
18. （6 分）如图，点 $O$ 是正方形 $ABCD$ 的中心。
（1）用直尺和圆规在正方形内部作一点 $E$（异于点 $O$），使得 $EB = EC$；（保留作图痕迹，不写作法）
（2）连接 $EB$，$EC$，$EO$。求证：$\angle BEO = \angle CEO$。

答案：

(1) 如图所示，点 $ E $ 即为所求。(答案不唯一)
　　　　　　　　　
(2) 连接 $ OB $，$ OC $。由
(1)得 $ EB = EC $。$ \because O $ 是正方形 $ ABCD $ 的中心，$ \therefore OB = OC $。在 $ \triangle EBO $ 和 $ \triangle ECO $ 中，$ \begin{cases} EB = EC, \\ EO = EO, \\ OB = OC, \end{cases} $ $ \therefore \triangle EBO \cong \triangle ECO(SSS) $，$ \therefore \angle BEO = \angle CEO $。