《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

20. (6分)有些大数值问题可以通过用字母代替数,转化成整式问题来解决,请先阅读下面的解题过程,再解答后面的问题.
例:若$x=123456789×123456786,y=123456788×123456787$,试比较x,y的大小.
解:设$123456788=a$,那么$x=(a+1)(a-2)=a^{2}-a-2,y=a(a-1)=a^{2}-a$,则$x-y=(a^{2}-a-2)-(a^{2}-a)=-2＜0$,所以$x＜y$.
看完后,你学会这种方法了吗? 再亲自试一试吧,你准行!
计算:$1.35×0.35×2.7-1.35^{3}-1.35×0.35^{2}$.

答案： 设$1.35=x$,则$2.7=2x,0.35=x-1,$
∴原式$=x(x-1)\cdot 2x-x^{3}-x(x-1)^{2}=2x^{3}-2x^{2}-x^{3}-x(x^{2}-2x+1)=-x=-1.35.$

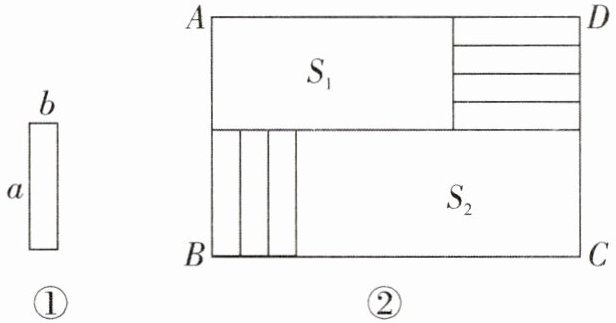
21. (7分)将7张相同的小长方形纸片(如图①所示)按图②所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为$S_{1},S_{2}$,已知小长方形纸片的长为a,宽为b,且$a＞b$.
(1)当$a=9,b=2,AD=30$时,求$S_{1}-S_{2}$的值;
(2)当$AD=30$时,请用含a,b的式子表示$S_{1}-S_{2}$的值;
(3)若AB长度不变,AD变长,将这7张小长方形纸片还按照同样的方式放在新的长方形ABCD内,而$S_{1}-S_{2}$的值总保持不变,求a,b满足的关系.

答案：
(1)$S_{1}-S_{2}=(30-9)×4×2-(30-3×2)×9=-48.$
(2)$S_{1}-S_{2}=4b(30-a)-a(30-3b)=120b-4ab-30a+3ab=120b-ab-30a.$
(3)$\because S_{1}-S_{2}=4b(AD-a)-a(AD-3b),$
整理,得$S_{1}-S_{2}=(4b-a)AD-ab.$
∵若AB长度不变,AD变长,而$S_{1}-S_{2}$的值总保持不变,$\therefore 4b-a=0$,解得$a=4b$.即a,b满足的关系是$a=4b.$