《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

17. 如图所示，已知∠CAE=65°，∠E=70°，且 AD⊥BC，如果△ABC 经过旋转后与△ADE 重合.
(1)旋转中心是哪个点?
(2)旋转了多少度?
(3)∠BAC 的度数是多少?

答案：
(1) 旋转中心是点 A.
(2) 旋转的角度即为 $∠CAE = 65^{\circ}$.
(3) 根据旋转的性质知, $∠EAC = ∠BAD = 65^{\circ}, ∠C = ∠E = 70^{\circ}$.
设 $AD⊥BC$ 于点 F, 则 $∠AFB = 90^{\circ}$,
$∴$ 在 $Rt△ABF$ 中, $∠B = 90^{\circ} - ∠BAD = 25^{\circ}$,
$∴$ 在 $△ABC$ 中, $∠BAC = 180^{\circ} - ∠B - ∠C = 180^{\circ} - 25^{\circ} - 70^{\circ} = 85^{\circ}$, 即 $∠BAC$ 的度数为 $85^{\circ}$.

18. 如图，在平面直角坐标系 xOy 中，点 A 的坐标为(-2,0)，等边三角形 AOC 经过平移或轴对称或旋转都可得到△DOB.
(1)若△AOC 沿 x 轴向右平移得到△OBD，则平移的距离是________个单位长度；若△AOC 与△BOD 关于直线对称，则对称轴是________；若△AOC 绕原点 O 顺时针旋转得到△DOB，则旋转角可以是________度.
(2)连接 AD，交 OC 于点 E，求∠AEO 的度数.

答案：

(1) 2 y 轴 120(最后一空答案不唯一)
(2) 如图, 连接 CD.
由已知得 $AO = AC = CD = OD$,
$∴$ 四边形 AODC 为菱形,
$∴OC⊥AD$, 即 $∠AEO = 90^{\circ}$.

19. 如图，已知平行四边形 ABCD 中，AB⊥AC，AB=1，BC=$\sqrt{5}$，对角线 AC，BD 交于点 O，将直线 AC 绕点 O 顺时针旋转，分别交 BC，AD 于点 E，F.
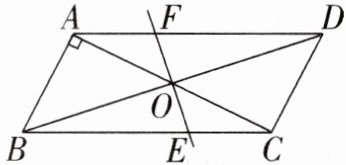
(1)证明：当旋转角为 90°时，四边形 ABEF 是平行四边形.
(2)试证明：在旋转过程中，线段 AF 与 EC 总保持相等.
(3)在旋转过程中，四边形 BEDF 可能是菱形吗? 如果不能，请说明理由；如果能，说明理由并求出此时 AC 绕点 O 顺时针旋转的度数.

答案：
(1) 当 $∠AOF = 90^{\circ}$ 时, $AB // EF$,
又 $AF // BE$,
$∴$ 四边形 ABEF 为平行四边形.
(2) $∵$ 四边形 ABCD 为平行四边形,
$∴AO = CO, ∠FAO = ∠ECO, ∠AOF = ∠COE$,
$∴\triangle AOF \cong \triangle COE, ∴AF = EC$.
(3) 四边形 BEDF 可能是菱形.
理由: 连接 BF, DE,
由
(2) 知 $△AOF \cong \triangle COE$, 得 $OE = OF$,
$∴EF$ 与 BD 互相平分.
当 $EF⊥BD$ 时, 四边形 BEDF 为菱形.
在 $Rt△ABC$ 中, $AC = \sqrt{5 - 1} = 2$,
$∴OA = 1 = AB$.
又 $AB⊥AC, ∴∠AOB = 45^{\circ}$,
$∴∠AOF = 45^{\circ}$,
$∴AC$ 绕点 O 顺时针旋转 $45^{\circ}$ 时, 四边形 BEDF 为菱形.