《2025年暑假总动员宁夏人民教育出版社八升九数学苏科版》

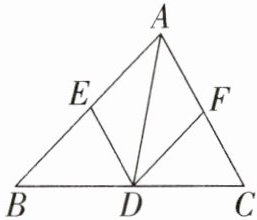
19. （6 分）如图，已知点 $D$ 在 $\triangle ABC$ 的 $BC$ 边上，$DE // AC$ 交 $AB$ 于点 $E$，$DF // AB$ 交 $AC$ 于点 $F$。
（1）求证：$AE = DF$；
（2）若 $AD$ 平分 $\angle BAC$，试判断四边形 $AEDF$ 的形状，并说明理由。

答案：
(1) $ \because DE // AC $，$ DF // AB $，$ \therefore $ 四边形 $ AEDF $ 是平行四边形，$ \therefore AE = DF $。
(2) 若 $ AD $ 平分 $ \angle BAC $，则四边形 $ AEDF $ 是菱形。
理由：$ \because AD $ 平分 $ \angle BAC $，$ \therefore \angle EAD = \angle FAD $。$ \because DE // AC $，$ \therefore \angle ADE = \angle FAD $，$ \therefore \angle EAD = \angle ADE $，$ \therefore AE = DE $。$ \because $ 四边形 $ AEDF $ 是平行四边形，$ \therefore $ 四边形 $ AEDF $ 是菱形。

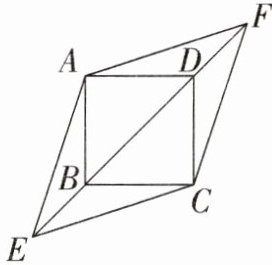
20. （6 分）如图，在正方形 $ABCD$ 中，对角线 $BD$ 所在的直线上有两点 $E$，$F$ 满足 $BE = DF$，连接 $AE$，$AF$，$CE$，$CF$。
（1）求证：$\triangle ABE \cong \triangle ADF$；
（2）试判断四边形 $AECF$ 的形状，并说明理由。

答案：

(1) $ \because $ 正方形 $ ABCD $，$ \therefore AB = AD $，$ \therefore \angle ABD = \angle ADB $，$ \therefore \angle ABE = \angle ADF $。在 $ \triangle ABE $ 与 $ \triangle ADF $ 中，$ \begin{cases} AB = AD, \\ \angle ABE = \angle ADF, \\ BE = DF, \end{cases} $ $ \therefore \triangle ABE \cong \triangle ADF(SAS) $。
(2) 四边形 $ AECF $ 是菱形。
理由：如图，连接 $ AC $，交 $ BD $ 于点 $ O $。
　　　　　　　　　　　　　　　
$ \because $ 四边形 $ ABCD $ 为正方形，$ \therefore OA = OC $，$ OB = OD $，$ AC \perp EF $，$ \therefore OB + BE = OD + DF $，即 $ OE = OF $。$ \because OA = OC $，$ OE = OF $，$ \therefore $ 四边形 $ AECF $ 是平行四边形。$ \because AC \perp EF $，$ \therefore $ 四边形 $ AECF $ 是菱形。

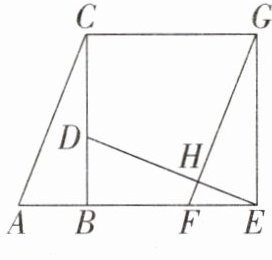
21. （6 分）如图，已知 $Rt\triangle ABC$ 中，$\angle ABC = 90^{\circ}$，先把 $\triangle ABC$ 绕点 $B$ 顺时针旋转 $90^{\circ}$ 至 $\triangle DBE$ 后，再把 $\triangle ABC$ 沿射线 $AB$ 平移至 $\triangle FEG$，$DE$，$FG$ 相交于点 $H$。
（1）判断线段 $DE$，$FG$ 的位置关系，并说明理由；
（2）连接 $CG$，求证：四边形 $CBEG$ 是正方形。

答案：
(1) $ FG \perp ED $。理由如下：$ \because \triangle ABC $ 绕点 $ B $ 顺时针旋转 $ 90^{\circ} $ 至 $ \triangle DBE $，$ \therefore \angle DEB = \angle ACB $。$ \because $ 把 $ \triangle ABC $ 沿射线 $ AB $ 平移至 $ \triangle FEG $，$ \therefore \angle GFE = \angle A $。$ \because \angle ABC = 90^{\circ} $，$ \therefore \angle A + \angle ACB = 90^{\circ} $，$ \therefore \angle DEB + \angle GFE = 90^{\circ} $，$ \therefore \angle FHE = 90^{\circ} $，$ \therefore FG \perp ED $。
(2) 根据旋转和平移可得 $ \angle GEF = 90^{\circ} $，$ \angle CBE = 90^{\circ} $，$ CG // EB $，$ CB = BE $。$ \because CG // EB $，$ \therefore \angle BCG = \angle CBE = 90^{\circ} $，$ \therefore $ 四边形 $ BCGE $ 是矩形。$ \because CB = BE $，$ \therefore $ 四边形 $ CBEG $ 是正方形。

22. （6 分）如图，在 $\triangle ABC$ 中，点 $O$ 是边 $AC$ 上一个动点，过点 $O$ 作直线 $EF // BC$ 分别交 $\angle ACB$，$\angle ACD$ 的平分线于点 $E$，$F$。
（1）若 $CE = 8$，$CF = 6$，求 $OC$ 的长；
（2）连接 $AE$，$AF$。问：当点 $O$ 在边 $AC$ 上运动到什么位置时，四边形 $AECF$ 是矩形？

答案：
(1) $ OC = \frac{1}{2}EF = 5 $。
(2) 当点 $ O $ 在边 $ AC $ 上运动到 $ AC $ 中点时，四边形 $ AECF $ 是矩形。