《2025年全品学练考九年级数学上册苏科版江苏专版》

6. A,B,C三种糖果的售价分别为每千克10元、11元、14元,若将A种糖果3kg,B种糖果2kg,C种糖果1kg混在一起,则售价应定为每千克11元.

答案： 11

7. 某校举办七年级数学素养大赛,比赛共设四个项目:速算比赛、数学推理、七巧拼图、魔方复原,每个项目得分(分值都为整数)都按一定百分比折算后计入总分.甲、乙、丙三位同学的速算比赛得分均为72分,七巧拼图得分均为78分且此两项在总分中所占百分比相等,其余两项得分如图3-1-4所示(单位:分).
(1)甲、乙、丙三位同学的速算比赛与七巧拼图项经折算后的得分和均为30分,求这两项在计入总分时所占的百分比;
(2)在(1)的条件下,据悉乙、丙两位同学的总分分别为74分和82分,请求出数学推理和魔方复原所占的百分比;
(3)在(1)和(2)的条件下,如果甲获得了第一名(甲、乙、丙的分数均不相同),那么甲的魔方复原至少获得______71分.

答案：
(1)20%
(2)数学推理和魔方复原所占的百分比分别为 40%,20%
(3)71

8. 核心素养数据意识某公司欲招聘一名销售人员,按1:3的比例入围的甲、乙、丙(笔试成绩没有相同的,按从高到低排列)三位入围者的成绩(百分制,成绩都是整数)如下表:

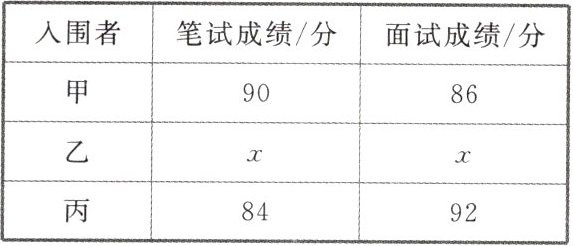
(1)若该公司认为笔试成绩与面试成绩同等重要,结果乙被录取,求x的值;89
(2)若该公司认为笔试成绩与面试成绩按4:6的权重,结果乙排第二,丙被录取,求x的值;88
(3)若该公司认为笔试成绩与面试成绩按$a:(10 - a)$(a为1~9的整数)的权重,为确保甲被录取,求a的最小值.8

答案：
(1)89
(2)88
(3)甲的最终成绩为 $\frac{90a + 86(10 - a)}{a + 10 - a} = (0.4a + 86)$ 分，
乙的最终成绩为 $x$ 分，
丙的最终成绩为 $\frac{84a + 92(10 - a)}{a + 10 - a} = (92 - 0.8a)$ 分.
又由题意，得 $x$ 最大为 89，
∴要确保甲被录取，
则 $\begin{cases}0.4a + 86 ＞ 92 - 0.8a \\ 0.4a + 86 ＞ 89\end{cases}$，
解得 $a ＞ 7.5$.
又
∵$a$ 为 $1 \sim 9$ 的整数，
∴$a$ 的最小值为 8.