《2025年全品学练考九年级数学上册苏科版江苏专版》

13. 如图2-4-13,$\odot O$的弦AB,CD的延长线相交于点P,且$AB= CD$。求证：$PA= PC$。

答案：
证明:如图，连接AC.
　　　　　
　
∵AB = CD,
∴$\overset{\frown}{AB} = \overset{\frown}{CD}$.
　
∴$\overset{\frown}{AB} + \overset{\frown}{BD} = \overset{\frown}{CD} + \overset{\frown}{BD}$，即$\overset{\frown}{AD} = \overset{\frown}{CB}$.则∠C = ∠A.
　
∴PA = PC.

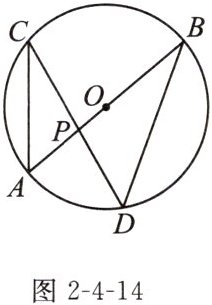
14. 如图2-4-14,在半径为5cm的$\odot O$中,直径AB与弦CD相交于点P,$∠CAB= 50^{\circ }$,$∠APD= 80^{\circ }$。
(1)求$∠ABD$的度数；(30°)
(2)求弦BD的长。(5$\sqrt{3}$cm)

答案：
(1)30°　
(2)5$\sqrt{3}$cm

15. 核心素养推理能力如图2-4-15,在$\odot O$中,P为$\overset{\frown }{AB}$的中点,弦AD,PC互相垂直,垂足为M,BC分别与AD,PD相交于点E,N,连接BD,MN。
(1)求证：N为BE的中点；
(2)若$\odot O$的半径为8,$\overset{\frown }{AB}的度数为90^{\circ }$,求线段MN的长。

答案：
解:
(1)证明:
∵AD⊥PC,
　
∴∠EMC = 90°.
　
∵P为$\overset{\frown}{AB}$的中点，
　
∴$\overset{\frown}{PA} = \overset{\frown}{PB}$.
　
∴∠ADP = ∠BDP = ∠BCP.
　　又
∵∠CEM = ∠DEN,
　
∴∠DNE = ∠EMC = 90°,
　
∴∠DNB = 90°.
　
∴∠DNE = ∠DNB.
　　又
∵∠EDN = ∠BDN,
　
∴∠DEN = ∠DBN.
　　则DE = DB.
∴EN = BN.
　
∴N为BE的中点.
(2)如图，连接OA,OB,AB,AC.
　　　　　　
　
∵$\overset{\frown}{AB}$的度数为90°,
∴∠AOB = 90°.
∵OA = OB = 8,
∴AB = 8$\sqrt{2}$
　　由
(1)同理得AM = EM.
　　又
∵EN = BN,
　
∴MN是△AEB的中位线.
　
∴MN = $\frac{1}{2}$AB = 4$\sqrt{2}$