《2025年全品学练考九年级数学上册苏科版江苏专版》

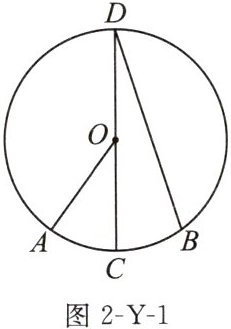
1. (2024 云南)如图 2-Y-1,CD 是$\odot O$的直径,点 A,B 在$\odot O$上.若$\widehat {AC}= \widehat {BC},∠AOC= 36^{\circ }$,则$∠D=$(B)

A.$9^{\circ }$
B.$18^{\circ }$
C.$36^{\circ }$
D.$45^{\circ }$

答案： B

2. (2024 贵州)如图 2-Y-2,在扇形纸扇中,若$∠AOB= 150^{\circ },OA= 24$,则$\widehat {AB}$的长为(C)
A.$30π$
B.$25π$
C.$20π$
D.$10π$

答案： C

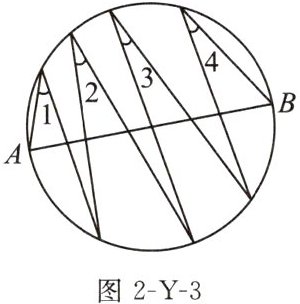
3. (2024 连云港)如图 2-Y-3,AB 是圆的直径,$∠1,∠2,∠3,∠4$的顶点均在 AB 上方的圆弧上,$∠1,∠4$的一边分别经过点 A,B,则$∠1+∠2+∠3+∠4= $90$^{\circ }$.

答案： 90

4. (2024 盐城)如图 2-Y-4,$△ABC是\odot O$的内接三角形,$∠C= 40^{\circ }$,连接 OA,OB,则$∠OAB= $______$^{\circ }$.

50

答案： 50

5. (2024 镇江)如图 2-Y-5,AB 是$\odot O$的内接正n边形的一边,点 C 在$\odot O$上,$∠ACB= 18^{\circ }$,则$n=$10.

答案： 10

6. (2024 常州)如图 2-Y-6,AB 是$\odot O$的直径,CD 是$\odot O$的弦,连接 AD,BC,BD.若$∠BCD= 20^{\circ }$,则$∠ABD= $______70$^{\circ }$.

答案： 70

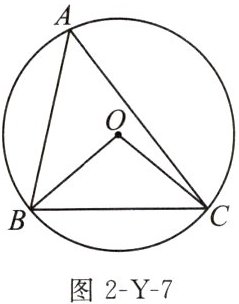
7. (2024 淮安)如图 2-Y-7,$△ABC是\odot O$的内接三角形,$∠BAC= 50^{\circ },\odot O$的半径为 3,则$\widehat {BC}$的长为______$\frac{5}{3}\pi$.

答案： $\frac{5}{3}\pi$

8. (2024 宿迁)如图 2-Y-8,已知正六边形 ABC-DEF 的边长为 2,以点 E 为圆心,EF 长为半径作圆,则该圆被正六边形截得的$\widehat {DF}$的长为$\frac{4\pi}{3}$.

答案： 1. 首先求圆心角$\angle DEF$的度数：
对于正$n$边形，其内角和公式为$(n - 2)×180^{\circ}$，正六边形$n = 6$，则内角和$(6 - 2)×180^{\circ}=720^{\circ}$。
每个内角$\angle DEF=\frac{(6 - 2)×180^{\circ}}{6}=120^{\circ}$。
2. 然后根据弧长公式$l=\frac{n\pi r}{180}$（$n$是圆心角弧度数，$r$是半径）求弧长：
已知半径$r = EF=2$，圆心角$n = 120^{\circ}$。
把$n = 120$，$r = 2$代入弧长公式$l=\frac{n\pi r}{180}$，可得$l=\frac{120\pi×2}{180}=\frac{4\pi}{3}$。
故该圆被正六边形截得的$\widehat{DF}$的长为$\frac{4\pi}{3}$。

9. (2024 镇江)如图 2-Y-9,将$△ABC$沿过点 A 的直线翻折并展开,点 C 的对应点$C'$落在边 AB 上,折痕为 AD,点 O 在边 AB 上,$\odot O$经过点 A,D.若$∠ACB= 90^{\circ }$,判断 BC 与$\odot O$的位置关系,并说明理由.
BC 与$\odot O$相切

答案： 1. 首先，连接$OD$：
因为$\triangle ADC$与$\triangle ADC'$关于$AD$对称，所以$\angle CAD=\angle C'AD$。
又因为$OA = OD$（$\odot O$的半径），根据等腰三角形的性质$\angle OAD=\angle ODA$。
2. 然后，进行等量代换：
由$\angle CAD=\angle C'AD$和$\angle OAD=\angle ODA$，可得$\angle CAD=\angle ODA$。
根据内错角相等，两直线平行，所以$OD// AC$。
3. 最后，判断直线$BC$与$\odot O$的位置关系：
已知$\angle ACB = 90^{\circ}$，即$AC\perp BC$。
因为$OD// AC$，根据平行线的性质（若一条直线垂直于一组平行线中的一条直线，则它也垂直于另一条直线），所以$OD\perp BC$。
又因为$OD$是$\odot O$的半径，根据直线与圆相切的判定定理（经过半径的外端并且垂直于这条半径的直线是圆的切线），所以$BC$与$\odot O$相切。
综上，$BC$与$\odot O$的位置关系是相切。