《2025年全品学练考九年级数学上册苏科版江苏专版》

1. (2024 凉山州)若关于 $ x $ 的一元二次方程 $ (a + 2)x^{2}+x + a^{2}-4 = 0 $ 的一个根是 $ x = 0 $,则 $ a $ 的值为(A)
A. 2
B. -2
C. 2 或 -2
D. $ \frac{1}{2} $

答案： A

2. (2024 上海)以下一元二次方程有两个相等实数根的是(D)
A. $ x^{2}-6x = 0 $
B. $ x^{2}-9 = 0 $
C. $ x^{2}-6x + 6 = 0 $
D. $ x^{2}-6x + 9 = 0 $

答案： D

3. (2024 淮安)若关于 $ x $ 的一元二次方程 $ x^{2}-4x + k = 0 $ 有两个不相等的实数根,则 $ k $ 的取值范围是(D)
A. $ k \geqslant 4 $
B. $ k ＞ 4 $
C. $ k \leqslant 4 $
D. $ k ＜ 4 $

答案： D

4. (2024 广安)若关于 $ x $ 的一元二次方程 $ (m + 1)x^{2}-2x + 1 = 0 $ 有两个不相等的实数根,则 $ m $ 的取值范围是(A)
A. $ m ＜ 0 $ 且 $ m \neq -1 $
B. $ m \geqslant 0 $
C. $ m \leqslant 0 $ 且 $ m \neq -1 $
D. $ m ＜ 0 $

答案： A

5. (2024 宿迁)规定：对于任意实数 $ a,b,c $,有【$ a,b $】$ c = ac + b $,其中等式右面是通常的乘法和加法运算,如【2,3】1 = $ 2 × 1 + 3 = 5 $。若关于 $ x $ 的方程【$ x,x + 1 $】$ (mx) = 0 $ 有两个不相等的实数根,则 $ m $ 的取值范围为(D)
A. $ m ＜ \frac{1}{4} $
B. $ m ＞ \frac{1}{4} $
C. $ m ＞ \frac{1}{4} $ 且 $ m \neq 0 $
D. $ m ＜ \frac{1}{4} $ 且 $ m \neq 0 $

答案： D

6. (2024 重庆 B 卷)重庆在低空经济领域实现了新的突破.今年第一季度低空飞行航线安全运行了 200 架次,预计第三季度低空飞行航线安全运行将达到 401 架次.设第二、第三两个季度安全运行架次的平均增长率为 $ x $,根据题意,可列方程为$200(1 + x)^2 = 401$.

答案： $200(1 + x)^2 = 401 $

7. (2024 深圳)一元二次方程 $ x^{2}-4x + a = 0 $ 的一个解为 $ x = 1 $,则 $ a = $3.

答案： 3

8. (2024 河南)若关于 $ x $ 的方程 $ \frac{1}{2}x^{2}-x + c = 0 $ 有两个相等的实数根,则 $ c $ 的值为______$ \frac{1}{2} $.

答案： $ \frac{1}{2} $

9. (2024 南充)已知 $ m $ 是方程 $ x^{2}+4x - 1 = 0 $ 的一个根,则 $ (m + 5)(m - 1) $ 的值为______-4.

答案： -4

10. (2024 泸州)已知 $ x_{1},x_{2} $ 是一元二次方程 $ x^{2}-3x - 5 = 0 $ 的两个实数根,则 $ (x_{1}-x_{2})^{2}+3x_{1}x_{2} $ 的值是______14.

答案： 14

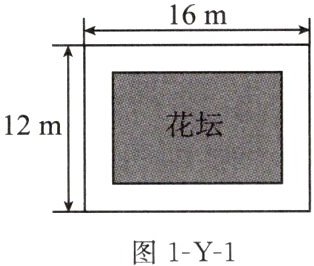
11. (2024 青岛)如图 1-Y-1,某小区要在长为 16 m、宽为 12 m 的矩形空地上建造一个花坛,使花坛四周小路的宽度相等,且花坛所占面积为空地面积的一半,则小路的宽为2m.

答案： 2

12. 解方程：
(1)(2024 滨州) $ x^{2}-4x = 0 $；$ x_1 = 0 $，$ x_2 = 4 $
(2)(2024 无锡) $ (x - 2)^{2}-4 = 0 $.$ x_1 = 4 $，$ x_2 = 0 $

答案：
(1)$ x_1 = 0 $，$ x_2 = 4 $
(2)$ x_1 = 4 $，$ x_2 = 0 $