《2025年全品学练考九年级数学上册苏科版江苏专版》

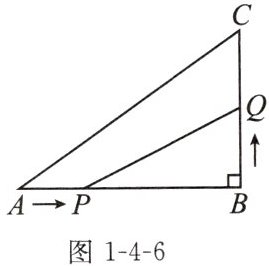
1. (2024南京期末)如图1-4-6,在$\triangle ABC$中,$\angle ABC= 90^{\circ}$,$AB= 8\mathrm{cm}$,$BC= 6\mathrm{cm}$,动点$P$,$Q分别从点A$,$B$同时开始移动(移动方向如图所示),点$P的速度为1\mathrm{cm}/\mathrm{s}$,点$Q的速度为2\mathrm{cm}/\mathrm{s}$,点$Q移动到点C$后停止,点$P$也随之停止移动,当$\triangle PBQ的面积为15\mathrm{cm}^{2}$时,点$P$移动的时间为______3s.

答案： 1. 首先，设点$P$移动的时间为$t$秒：
已知点$P$的速度为$1\mathrm{cm}/\mathrm{s}$，则$AP = t\mathrm{cm}$，那么$PB=(8 - t)\mathrm{cm}$；
点$Q$的速度为$2\mathrm{cm}/\mathrm{s}$，则$BQ = 2t\mathrm{cm}$。
因为$\angle ABC = 90^{\circ}$，根据三角形面积公式$S=\frac{1}{2}ah$（这里$a = BQ$，$h = PB$），所以${S}_{\triangle PBQ}=\frac{1}{2}PB\cdot BQ$。
2. 然后，将$PB=(8 - t)\mathrm{cm}$，$BQ = 2t\mathrm{cm}$代入面积公式：
已知${S}_{\triangle PBQ}=15\mathrm{cm}^{2}$，则$\frac{1}{2}(8 - t)×2t = 15$。
化简方程：
方程$\frac{1}{2}(8 - t)×2t = 15$可化为$(8 - t)t = 15$。
展开得$8t-t^{2}=15$。
移项化为一元二次方程的一般形式$t^{2}-8t + 15 = 0$。
3. 接着，求解一元二次方程$t^{2}-8t + 15 = 0$：
对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$，这里$a = 1$，$b=-8$，$c = 15$，根据因式分解法$t^{2}-8t + 15=(t - 3)(t - 5)=0$。
则$t - 3 = 0$或$t - 5 = 0$。
解得$t_{1}=3$，$t_{2}=5$。
4. 最后，检验$t$的值：
因为点$Q$移动到点$C$停止，$BC = 6\mathrm{cm}$，点$Q$速度为$2\mathrm{cm}/\mathrm{s}$，所以$Q$移动的时间$t_{Q}=\frac{6}{2}=3\mathrm{s}$。
当$t = 5$时，$BQ=2t = 10\gt6$，不符合题意，舍去。
所以点$P$移动的时间为$3\mathrm{s}$。

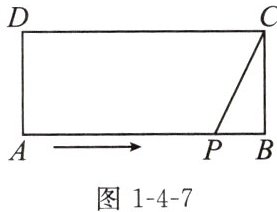
2. 如图1-4-7,在矩形$ABCD$中,$AB= 9\mathrm{cm}$,$BC= \sqrt{15}\mathrm{cm}$,点$P从点A出发沿AB以1\mathrm{cm}/\mathrm{s}的速度向点B$移动. 点$P$出发8秒后,点$P$,$A的距离是点P$,$C的距离的2$倍?

答案： 解：设点$P$出发$t$秒后，点$P$，$A$的距离是点$P$，$C$的距离的$2$倍。
已知点$P$从点$A$出发沿$AB$以$1cm/s$的速度向点$B$移动，则$AP = t cm$，$PB=(9 - t)cm$。
在矩形$ABCD$中，$BC = \sqrt{15}cm$，根据勾股定理，$PC^{2}=PB^{2}+BC^{2}=(9 - t)^{2}+(\sqrt{15})^{2}$。
因为$AP = 2PC$，所以$AP^{2}=4PC^{2}$，即$t^{2}=4[(9 - t)^{2}+(\sqrt{15})^{2}]$。
展开式子得：$t^{2}=4(81-18t+t^{2}+15)$
$t^{2}=4(96-18t+t^{2})$
$t^{2}=384-72t + 4t^{2}$
移项得：$4t^{2}-t^{2}-72t + 384 = 0$
$3t^{2}-72t + 384 = 0$
两边同时除以$3$得：$t^{2}-24t + 128 = 0$
对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$，这里$a = 1$，$b=-24$，$c = 128$，根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$，则$t=\frac{24\pm\sqrt{(-24)^{2}-4×1×128}}{2×1}=\frac{24\pm\sqrt{576 - 512}}{2}=\frac{24\pm\sqrt{64}}{2}=\frac{24\pm8}{2}$。
$t_{1}=\frac{24 + 8}{2}=16$，$t_{2}=\frac{24-8}{2}=8$。
因为$0\leq t\leq9$，所以$t = 8$。
答：点$P$出发$8$秒后，点$P$，$A$的距离是点$P$，$C$的距离的$2$倍。

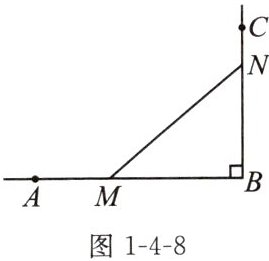
3. 如图1-4-8,$AB\perp BC$,$AB= 12\mathrm{cm}$,$BC= 8\mathrm{cm}$. 一只蝉从点$C沿CB方向以1\mathrm{cm}/\mathrm{s}$的速度爬行,一只螳螂为了捕捉这只蝉,同时从点$A沿AB方向以2\mathrm{cm}/\mathrm{s}$的速度爬行,一段时间后,它们分别到达了点$N$,$M$的位置. 若此时$\triangle MNB的面积为24\mathrm{cm}^{2}$,求它们爬行的时间.

它们爬行的时间为2 s.

答案： 解：设它们爬行的时间为$t$秒。
已知蝉从点$C$沿$CB$方向以$1cm/s$的速度爬行，则$CN = tcm$，那么$BN=(8 - t)cm$；
螳螂从点$A$沿$AB$方向以$2cm/s$的速度爬行，则$AM = 2tcm$，那么$BM=(12 - 2t)cm$。
因为$\triangle MNB$的面积为$24cm^{2}$，且$AB\perp BC$，根据三角形面积公式$S=\frac{1}{2}ah$（$a$为底，$h$为高），对于$\triangle MNB$，$a = BN$，$h = BM$，可得方程：
$\frac{1}{2}(8 - t)(12 - 2t)=24$
展开括号得：
$\frac{1}{2}(96-16t - 12t + 2t^{2})=24$
$48-14t + t^{2}=24$
移项化为一元二次方程的一般形式：$t^{2}-14t + 48 - 24 = 0$，即$t^{2}-14t + 24 = 0$
分解因式得$(t - 2)(t - 12)=0$
则$t - 2 = 0$或$t - 12 = 0$
解得$t_{1}=2$，$t_{2}=12$。
当$t = 12$时，$BM=12-2t=12-2×12=-12$（长度不能为负，舍去）。
所以它们爬行的时间为$2$秒。

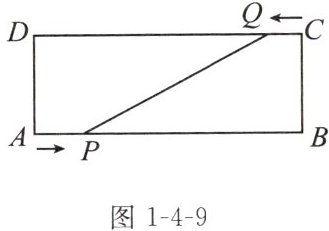
4. (教材复习题T14变式)如图1-4-9,在矩形$ABCD$中,$AB= 16\mathrm{cm}$,$BC= 6\mathrm{cm}$,点$P从点A出发沿AB边以3\mathrm{cm}/\mathrm{s}的速度向点B$移动,一直到达点$B$为止；同时,点$Q从点C出发沿CD边以2\mathrm{cm}/\mathrm{s}的速度向点D$移动. 设移动时间为$t\mathrm{s}$,连接$PQ$.
(1)当$t= 2$时,求$PQ$的长；$6\sqrt {2}cm$
(2)当$PQ= 10\mathrm{cm}$时,求$t$的值.1.6 或 4.8

答案： 1. （1）
解：
过点$P$作$PE\perp CD$于点$E$。
因为四边形$ABCD$是矩形，所以$\angle A=\angle D = 90^{\circ}$，$AB// CD$，则四边形$APED$是矩形，所以$PE = AD=BC = 6\mathrm{cm}$，$DE = AP$。
已知$AP = 3t\mathrm{cm}$，$CQ = 2t\mathrm{cm}$，当$t = 2$时，$AP=3×2 = 6\mathrm{cm}$，$CQ = 2×2 = 4\mathrm{cm}$。
则$EQ=CD - DE - CQ$，又因为$CD = AB = 16\mathrm{cm}$，$DE = AP$，所以$EQ=16 - 6 - 4=6\mathrm{cm}$。
在$Rt\triangle PEQ$中，根据勾股定理$PQ=\sqrt{PE^{2}+EQ^{2}}$，把$PE = 6\mathrm{cm}$，$EQ = 6\mathrm{cm}$代入可得：
$PQ=\sqrt{6^{2}+6^{2}}=\sqrt{36 + 36}=\sqrt{72}=6\sqrt{2}\mathrm{cm}$。
2. （2）
解：
由（1）可知$PE = 6\mathrm{cm}$，$EQ=16-(3t + 2t)=16 - 5t\mathrm{cm}$。
在$Rt\triangle PEQ$中，根据勾股定理$PQ^{2}=PE^{2}+EQ^{2}$，已知$PQ = 10\mathrm{cm}$，$PE = 6\mathrm{cm}$，则$10^{2}=6^{2}+(16 - 5t)^{2}$。
即$100=36+(16 - 5t)^{2}$，移项可得$(16 - 5t)^{2}=100 - 36 = 64$。
所以$16-5t=\pm8$。
当$16-5t = 8$时：
$ - 5t=8 - 16$，$-5t=-8$，解得$t=\frac{8}{5}$。
当$16-5t=-8$时：
$-5t=-8 - 16$，$-5t=-24$，解得$t=\frac{24}{5}$。
综上，（1）$PQ$的长为$6\sqrt{2}\mathrm{cm}$；（2）$t$的值为$\frac{8}{5}$或$\frac{24}{5}$。