第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
1. 下列条件中,能确定圆的是 (
A. 以已知点O为圆心画圆
B. 以1 cm为半径画圆
C. 经过已知点A,且以2 cm为半径画圆
D. 以点O为圆心,1 cm为半径画圆
D
)A. 以已知点O为圆心画圆
B. 以1 cm为半径画圆
C. 经过已知点A,且以2 cm为半径画圆
D. 以点O为圆心,1 cm为半径画圆
答案:
D
2. 到圆心的距离不大于半径的点的集合是(
A. 圆的外部
B. 圆的内部
C. 圆
D. 圆的内部和圆
D
)A. 圆的外部
B. 圆的内部
C. 圆
D. 圆的内部和圆
答案:
D
3. 已知$\odot O$的半径为5,点P在$\odot O$内,则OP的长可能是 (
A. 7
B. 6
C. 5
D. 4
D
)A. 7
B. 6
C. 5
D. 4
答案:
D
4. (2023南京期中)已知$\odot O$的半径为3,平面内点P到圆心O的距离为$\sqrt{5}$,则点P与$\odot O$的位置关系是 (
A. 点P在$\odot O$外
B. 点P在$\odot O$上
C. 点P在$\odot O$内
D. 无法确定
C
)A. 点P在$\odot O$外
B. 点P在$\odot O$上
C. 点P在$\odot O$内
D. 无法确定
答案:
C
5. 如图2-1-1,已知$\odot O$的半径为3,平面内有一点到圆心O的距离为5,则此点可能是(
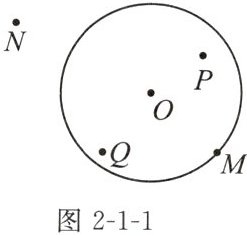
A. 点P
B. 点Q
C. 点M
D. 点N
D
)
A. 点P
B. 点Q
C. 点M
D. 点N
答案:
D
6. 平面内到点P的距离等于2 cm的点的集合是
以点 P 为圆心,2 cm 为半径的圆
.
答案:
以点 P 为圆心,2 cm 为半径的圆
7. 若点A到$\odot O$上的点的最大距离为5 cm,最小距离为3 cm,则$\odot O$的半径为
4 或 1
cm.
答案:
4 或 1
8. 已知$\odot N$的半径为3,点M与点N之间的距离为d,且关于x的方程$x^{2}-2\sqrt{3}x+d= 0$有两个相等的实数根,则点M与$\odot N$的位置关系是
点 M 在⊙N 上
.
答案:
点 M 在⊙N 上
9. 平面直角坐标系中,以原点O为圆心,2为半径作$\odot O$,则点A(2,2)与$\odot O$的位置关系为
点 A 在⊙O 外
.
答案:
点 A 在⊙O 外
10. 如图2-1-2,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AC= 2$ cm,$BC= 4$ cm,CM为中线.以点C为圆心,$\sqrt{5}$ cm为半径作圆,则A,B,M三点中在圆外的点是
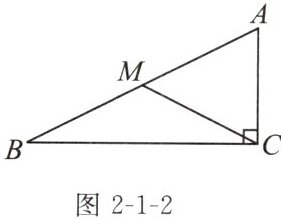
B
、在圆上的点是M
、在圆内的点是A
.请说明理由.
答案:
解:在圆外的是点 B,在圆上的是点 M,在圆内的是点 A. 理由如下:
∵∠ACB = 90°,AC = 2 cm,BC = 4 cm,
∴AB = $\sqrt{AC^{2}+BC^{2}}=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$(cm).
∵CM 是中线,
∴CM = $\frac{1}{2}AB=\sqrt{5}$ cm.
∴点 M 在圆上.
∵AC = 2 cm < $\sqrt{5}$ cm,
∴点 A 在圆内.
∵BC = 4 cm > $\sqrt{5}$ cm,
∴点 B 在圆外.
∵∠ACB = 90°,AC = 2 cm,BC = 4 cm,
∴AB = $\sqrt{AC^{2}+BC^{2}}=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$(cm).
∵CM 是中线,
∴CM = $\frac{1}{2}AB=\sqrt{5}$ cm.
∴点 M 在圆上.
∵AC = 2 cm < $\sqrt{5}$ cm,
∴点 A 在圆内.
∵BC = 4 cm > $\sqrt{5}$ cm,
∴点 B 在圆外.
11. 以坐标原点O为圆心,5为半径作圆,则下列各点中,一定在$\odot O$内的是 (
A. (3,3)
B. (3,4)
C. (4,4)
D. (4,5)
A
)A. (3,3)
B. (3,4)
C. (4,4)
D. (4,5)
答案:
A
12. 雷达通过无线电的方法发现目标并测定它们的空间位置,因此雷达被称为“无线电定位”.现有一款监测半径为5 km的雷达,监测点的分布情况如图2-1-3,如果将雷达装置设在P点,每一个小正方形的边长均为1 km,那么能被雷达监测到的最远的点为 (
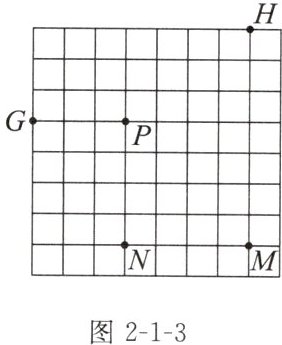
A. G
B. H
C. M
D. N
B
)
A. G
B. H
C. M
D. N
答案:
B
13. 已知点A的坐标为(2,0),点P在直线y= x上运动.当以点P为圆心,PA为半径的圆的面积最小时,点P的坐标为 (
A. (1,-1)
B. (0,0)
C. (1,1)
D. ($\sqrt{2}$,$\sqrt{2}$)
C
)A. (1,-1)
B. (0,0)
C. (1,1)
D. ($\sqrt{2}$,$\sqrt{2}$)
答案:
C
查看更多完整答案,请扫码查看


