《2025年全品学练考九年级数学上册苏科版江苏专版》

8. 已知$\odot O$的半径是4,圆心O到直线l的距离d为方程$x^{2}-4x-5= 0$的一个根,则$\odot O$与直线l的位置关系为相离．

答案： 相离

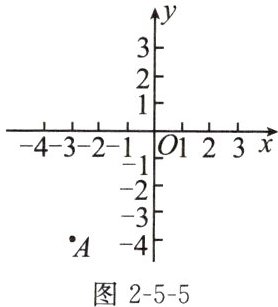
9. 如图2-5-5,在平面直角坐标系中有一点$A(-3,-4)$,以点A为圆心,r为半径的圆与坐标轴有3个交点,则$r=$4 或 5．

答案： 4 或 5

10. (2023无锡期中)如图2-5-6,在$Rt\triangle ABC$中,$\angle ACB= 90^{\circ}$,$\angle A= 60^{\circ}$,$AB= 10cm$,点D从点A出发,沿射线AB以2cm/s的速度移动,移动过程中始终保持$DE// BC$,$DF// AC$(点E,F分别在射线AC,CB上)．以点D为圆心,DE为半径作$\odot D$,若$\odot D$上恰好只有两个点到直线BC的距离为3cm,设点D移动的时间为t s,则t的取值范围是$ \sqrt{3} - 1 ＜ t ＜ 4\sqrt{3} - 4 $．

答案： $ \sqrt{3} - 1 ＜ t ＜ 4\sqrt{3} - 4 $

11. 如图2-5-7,$\angle AOB= 30^{\circ}$,点M在OB上,且$OM= 5cm$,以点M为圆心,r为半径画圆．讨论射线OA与$\odot M$的公共点个数,并写出r相应的取值范围．
当$ 0 \text{ cm} ＜ r ＜ 2.5 \text{ cm} $时，$\odot M$ 与射线 $ OA $ 没有公共点；当$ r = 2.5 \text{ cm} $ 或 $ r ＞ 5 \text{ cm} $时，$\odot M$ 与射线 $ OA $ 只有一个公共点；当$ 2.5 \text{ cm} ＜ r \leq 5 \text{ cm} $时，$\odot M$ 与射线 $ OA $ 有两个公共点

答案： 当 $ 0 \text{ cm} ＜ r ＜ 2.5 \text{ cm} $ 时，$\odot M$ 与射线 $ OA $ 没有公共点；当 $ r = 2.5 \text{ cm} $ 或 $ r ＞ 5 \text{ cm} $ 时，$\odot M$ 与射线 $ OA $ 只有一个公共点；当 $ 2.5 \text{ cm} ＜ r \leq 5 \text{ cm} $ 时，$\odot M$ 与射线 $ OA $ 有两个公共点

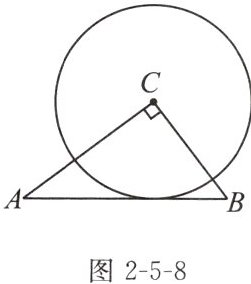
12. 如图2-5-8,在$\triangle ABC$中,$\angle C= 90^{\circ}$,$AC= 4$,$BC= 3$,以点C为圆心,r为半径画圆．
(1)当$r= $______时,$\odot C$与边AB相切；
(2)当r满足______时,$\odot C$与边AB只有一个公共点；
(3)随着r的变化,$\odot C$与边AB的公共点个数有哪些变化？写出相应的r的值或取值范围．

答案：
解：
(1) 如图①，过点 $ C $ 作 $ CD \perp AB $ 于点 $ D $.
$\because \angle ACB = 90^{\circ}$，$AC = 4$，$BC = 3$，
$\therefore AB = 5$.
当直线与 $\odot C$ 相切时，点 $ C $ 到直线 $ AB $ 的距离 $ d = r $，$\odot C$ 与斜边 $ AB $ 只有一个公共点.
$\because CD \cdot AB = AC \cdot BC$，
$\therefore CD = r = 2.4$.
故答案为 2.4.
　　
(2) 当直线与 $\odot C$ 相切时，即点 $ C $ 到直线 $ AB $ 的距离 $ d = r = 2.4 $，$\odot C$ 与斜边 $ AB $ 只有一个公共点；当直线与 $\odot C$ 的位置如图②所示时，也只有一个公共点，此时 $ 3 ＜ r \leq 4 $.
故答案为 $ 3 ＜ r \leq 4 $ 或 $ r = 2.4 $.
(3) 如图③，当 $ 0 ＜ r ＜ 2.4 $ 时，$\odot C$ 与边 $ AB $ 有 0 个公共点；

如图①，当 $ r = 2.4 $ 时，$\odot C$ 与边 $ AB $ 有 1 个公共点；
如图④，当 $ 2.4 ＜ r \leq 3 $ 时，$\odot C$ 与边 $ AB $ 有 2 个公共点；
如图②，当 $ 3 ＜ r \leq 4 $ 时，$\odot C$ 与边 $ AB $ 有 1 个公共点；
如图⑤，当 $ r ＞ 4 $ 时，$\odot C$ 与边 $ AB $ 有 0 个公共点.
综上所述，当 $ 0 ＜ r ＜ 2.4 $ 或 $ r ＞ 4 $ 时，$\odot C$ 与边 $ AB $ 有 0 个公共点；
当 $ 3 ＜ r \leq 4 $ 或 $ r = 2.4 $ 时，$\odot C$ 与边 $ AB $ 有 1 个公共点；
当 $ 2.4 ＜ r \leq 3 $ 时，$\odot C$ 与边 $ AB $ 有 2 个公共点.