《2025年全品学练考九年级数学上册苏科版江苏专版》

1. 近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,经销商纷纷开展降价促销活动.某款燃油汽车今年2月份的售价为36万元,4月份的售价为25万元,设该款汽车这两个月售价的平均月降价率是x,则所列方程正确的是 (C)
A. $25(1-2x)= 36$
B. $25(1+x)^{2}= 36$
C. $36(1-x)^{2}= 25$
D. $25(1-x)^{2}= 36$

答案： C

2. 某商店6月份的营业额为200万元,8月份的营业额达到242万元,则该商店这两个月的营业额的平均月增长率是 (A)
A. 10%
B. 12%
C. 15%
D. 20%

答案： A

3. (2023连云港期末)某汽车厂商经过两次增产,将汽车的产量由4.86万辆提高至6万辆,设平均每次增产的百分率是x,则可列方程为$ 4.86(1 + x)^2 = 6 $.

答案： $ 4.86(1 + x)^2 = 6 $

4. (2024泰州期末)一枚圆形古钱币的中间是一个边长为1cm的正方形孔,已知正方形面积是圆面积的$\frac {1}{9}$,设圆的半径为xcm,可得方程为$ \frac{1}{9}\pi x^2 = 1 $.

答案： $ \frac{1}{9}\pi x^2 = 1 $

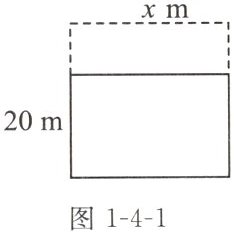
5. 现有一块矩形绿地(如图1-4-1),它的宽为20m,若将宽增大到与长相等(长不变),使扩大后绿地的形状为正方形,则扩大后绿地的面积比原来增加了$300m^{2}$.设扩大后的正方形绿地的边长为xm,可得方程为$ x(x - 20) = 300 $.

答案： $ x(x - 20) = 300 $

6. 如图1-4-2,某小区计划在一个长16m、宽9m的矩形场地ABCD上,修建三条同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草.若种草部分的总面积为$112m^{2}$,则小路的宽为1m.

答案： 1

7. (2022南京模拟)为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每盒零售价由16元降为9元,求平均每次降价的百分率.

答案： $ 25\% $

8. (2024南京期末)如图1-4-3,用篱笆围成一个矩形花圃,该花圃一面靠墙,而且中间有一道垂直于墙的隔栏(隔栏也用篱笆制作),已知所用篱笆的总长为24m,花圃的面积为$45m^{2}$,墙的最大可用长度为10m,求边AB的长.

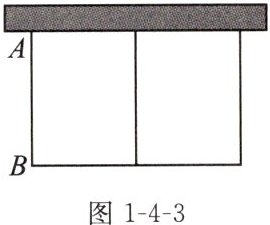
5m

答案： $ 5m $

9. (2024盐城期末)为了丰富全县学生的业余生活,县文体中心图书馆计划三个季度购进新书共21000册,已知第一个季度购进5000册,求县文体中心图书馆后两个季度购书的平均季增长率.若设后两个季度购书的平均季增长率为x,则根据题意可列方程为$ 5000 + 5000(1 + x) + 5000(1 + x)^2 = 21000 $.

答案： $ 5000 + 5000(1 + x) + 5000(1 + x)^2 = 21000 $