《2025年全品学练考九年级数学上册苏科版江苏专版》

13. (2024 南充)已知 $ x_{1},x_{2} $ 是关于 $ x $ 的方程 $ x^{2}-2kx + k^{2}-k + 1 = 0 $ 的两个不相等的实数根.
(1)求 $ k $ 的取值范围；
(2)若 $ k ＜ 5 $,且 $ k,x_{1},x_{2} $ 都是整数,求 $ k $ 的值.

答案：
(1)$ k ＞ 1 $
(2)2

14. (2024 扬州模拟)某初中学校要新建一块矩形篮球场地(如图 1-Y-2 所示),要求：①篮球场地的长和宽分别为 28 m 和 16 m；②在篮球场地四周修建宽度相等的安全区域；③篮球场地及安全区域的总面积为 $ 640 m^{2} $.
(1)求安全区域的宽度；2 m
(2)某公司希望用 50 万元承包这项工程,该学校认为金额太高需要降价,通过两次协商,最终以 32 万元达成一致.若两次降价的百分率相同,求每次降价的百分率.20%

答案：
(1)2 m
(2)20%

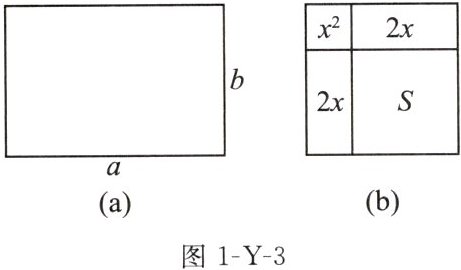
15. (2024 泰州模拟)大约于公元前 2000 年,古巴比伦人用“长”“宽”及“面积”来代表未知数及它们的乘积.如图 1-Y-3(a),长代表 $ a $、宽代表 $ b $,长方形的面积代表 $ ab $.大约于公元 820 年,阿尔·花拉子米(Al-Khwarizmi)在《代数学》中介绍了用几何学方式求方程的解.
(1)某实践小组对《代数学》的内容进行研习后,也尝试用几何学方式解 $ x^{2}+4x - 12 = 0(x ＞ 0) $,并进行以下操作步骤：
第一步：将方程变形成 $ x^{2}+4x = 12 $；
第二步：构造边长为 $ (x + 2) $ 的正方形(如图(b))；
第三步：求得右下角正方形面积 $ S $ 的值是①______；
第四步：用两种方法表示图中大正方形的面积：$ (x + 2)^{2}= x^{2}+2x + 2x + S $,将 $ x^{2}+4x = 12 $ 代入,可得 $ (x + 2)^{2}= $②______.
$ \because x ＞ 0 $,
$ \therefore x = $③______.
请补全该实践小组求解过程中①②③所缺的内容.
(2)请参照上述方法解方程 $ x^{2}+5x - 6 = 0(x ＞ 0) $.

答案：
解：
(1)①②③所缺的内容分别为16，2.
(2)第一步：将方程变形成$ x^2 + 5x = 6 $；
第二步：构造边长为$ (x + 2.5) $的正方形如图；

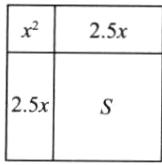
第三步：求得右下角正方形面积S的是$ S = (x + 2.5)^2 - x^2 - 2.5x - 2.5x = \frac{25}{4} $；
第四步：用两种方法表示图中大正方的面积：
$ (x + 2.5)^2 = x^2 + 2.5x + 2.5x + S $，
将$ x^2 + 5x = 6 $代入，可得$ (x + 2.5)^2 = \frac{49}{4} $，
$ \therefore x + 2.5 = \pm \frac{7}{2} $，
$ \therefore x_1 = 1 $，$ x_2 = -6 $.
$ \because x ＞ 0 $，$ \therefore x = 1 $.