《2025年全品学练考九年级数学上册苏科版江苏专版》

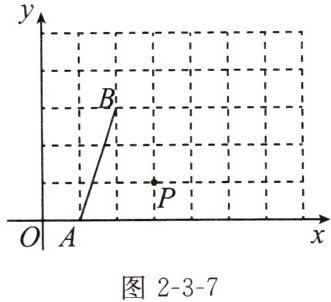
13. (2023 南京期末)如图 2-3-7,在平面直角坐标系 xOy 中,点 A,B,P 的坐标分别为(1,0),(2,3),(3,1).若点 C 在第一象限,且其横坐标、纵坐标均为整数,P 是△ABC 的外心,则点 C 的坐标为(4,3)或(5,2)或(1,2).

答案： $(4,3)$或$(5,2)$或$(1,2)$

14. (2024 宿迁月考)如图 2-3-8 所示,在平面直角坐标系中有△ABC,请在图中画出△ABC 的外接圆的圆心 P.
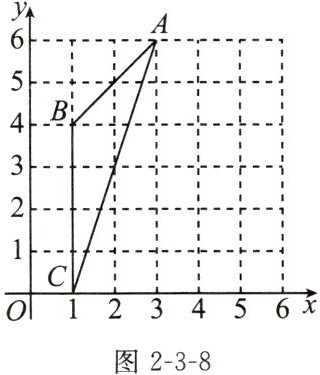
(1)圆心 P 的坐标是(5,2);
(2)判断点 M(6,5)是否在⊙P 上?点 M 不在⊙P 上

答案： 图略
(1)$(5,2)$
(2)点 $M$ 不在$\odot P$ 上

15. 如图 2-3-9,已知 AD 既是△ABC 的中线,又是角平分线.
(1)试判断△ABC 的形状,并说明理由;△ABC 是等腰三角形. 理由略
(2)直线 AD 是否过△ABC 外接圆的圆心?试证明你的结论.AD 过△ABC 外接圆的圆心.证明: ∵ AB = AC，AD 是△ABC 的角平分线，∴ AD ⊥ BC.又 ∵ BD = CD，∴ 直线 AD 是 BC 的垂直平分线，∴ 直线 AD 过△ABC 外接圆的圆心.

答案：
(1)$\triangle ABC$ 是等腰三角形. 理由略
(2)$AD$ 过$\triangle ABC$ 外接圆的圆心.
证明: $\because AB = AC$，$AD$ 是$\triangle ABC$ 的角平分线，$\therefore AD \perp BC$.
又 $\because BD = CD$，
$\therefore$ 直线 $AD$ 是 $BC$ 的垂直平分线，
$\therefore$ 直线 $AD$ 过$\triangle ABC$ 外接圆的圆心.

16. 设 x,y 是一个直角三角形两条直角边的长,且$(x^2+y^2)(x^2+y^2 - 1)= 56,$求这个直角三角形的外接圆面积.

答案： 解:设这个直角三角形的斜边长为 $z$.
由题意，得 $x^{2} + y^{2} = z^{2}$.
$\because (x^{2} + y^{2})(x^{2} + y^{2} - 1) = 56$，
$\therefore z^{2}(z^{2} - 1) = 56$.
令 $z^{2} = t$，则有 $t(t - 1) = 56$，
整理，得 $t^{2} - t - 56 = 0$，
解得 $t_{1} = 8$，$t_{2} = -7$(舍)，$\therefore z^{2} = 8$.
$\because z$ 为直角三角形的斜边长，
$\therefore z = 2\sqrt{2}$，
$\therefore$ 这个直角三角形的外接圆的直径为 $2\sqrt{2}$，半径为$\sqrt{2}$，
$\therefore$ 这个直角三角形的外接圆的面积为 $2\pi$.