《2025年全品学练考九年级数学上册苏科版江苏专版》

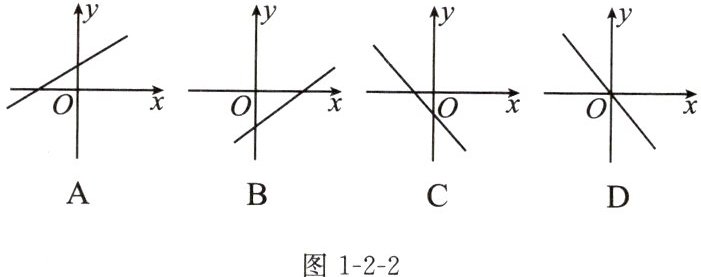
10. 若关于x的一元二次方程$x^{2}-2x+kb+1= 0$有两个不相等的实数根,则一次函数$y= kx+b$的图像可能是 (B)

答案： B

11. 已知关于x的一元二次方程$ax^{2}+2x+2-c= 0$有两个相等的实数根,则$\frac {1}{a}+c$的值为____2.

答案： 2

12. (2024南京期末)若关于x的方程$ax^{2}-4x-1= 0$有两个不相等的实数根,则a的取值范围是$ a ＞ - 4 $且$ a \neq 0 $.

答案： $ a ＞ - 4 $且$ a \neq 0 $

13. 已知关于x的一元二次方程$mx^{2}-2x+n-3= 0$有两个相等的实数根,则$\frac {1}{m}-n$的值是-3.

答案： -3

14. (2024扬州期末)已知关于x的方程$x^{2}-(k+2)x+2k= 0$.
(1)求证:无论k取何值,方程总有实数根;
(2)若方程有两个相等的实数根,求出方程的根.

答案： 解:
(1)证明:$ b ^ { 2 } - 4 a c = [ - ( k + 2 ) ] ^ { 2 } - 4 \cdot 2 k = ( k - 2 ) ^ { 2 } $.
$ \because ( k - 2 ) ^ { 2 } \geqslant 0 $,即$ b ^ { 2 } - 4 a c \geqslant 0 $,
$ \therefore $无论$ k $取何值,方程总有实数根.
(2)根据题意,得$ b ^ { 2 } - 4 a c = ( k - 2 ) ^ { 2 } = 0 $,
解得$ k = 2 $,
则方程变形为$ x ^ { 2 } - 4 x + 4 = 0 $,
$ \therefore x _ { 1 } = x _ { 2 } = 2 $.

15. 已知关于x的一元二次方程$x^{2}-(2k+1)x+k^{2}+k= 0$.
(1)求证:无论k取何值,方程都有两个不相等的实数根;
(2)如果方程的两个实数根分别为$x_{1},x_{2}$,且k与$\frac {x_{1}}{x_{2}}$都为整数,求k的所有可能的值.

答案： 解:
(1)证明:$ \because a = 1 $,$ b = - ( 2 k + 1 ) $,$ c = k ^ { 2 } + k $,$ b ^ { 2 } - 4 a c = [ - ( 2 k + 1 ) ] ^ { 2 } - 4 ( k ^ { 2 } + k ) = 1 ＞ 0 $,$ \therefore $无论$ k $取何值,方程都有两个不相等的实数根.
(2)$ \because b ^ { 2 } - 4 a c = 1 $,
$ \therefore x = \frac { 2 k + 1 \pm 1 } { 2 } $.
$ \therefore $一元二次方程$ x ^ { 2 } - ( 2 k + 1 ) x + k ^ { 2 } + k = 0 $的两个根分别为$ k + 1 $,$ k $.
$ \therefore \frac { x _ { 1 } } { x _ { 2 } } = \frac { k + 1 } { k } = 1 + \frac { 1 } { k } $或$ \frac { x _ { 1 } } { x _ { 2 } } = \frac { k } { k + 1 } = 1 - \frac { 1 } { k + 1 } $.
若$ 1 + \frac { 1 } { k } $为整数,则$ k $为1的约数,
$ \therefore k = \pm 1 $.
若$ 1 - \frac { 1 } { k + 1 } $为整数,则$ k + 1 $为1的约数,
$ \therefore k + 1 = \pm 1 $,则$ k $为0或-2.
综上所述,整数$ k $的所有可能的值为$ \pm 1 $,0或-2.