《2025年全品学练考九年级数学上册苏科版江苏专版》

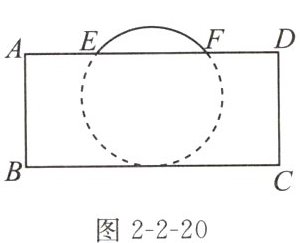
10. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图2-2-20,已知$EF= CD= 8cm$,则球的半径长是______5cm.

答案： 5cm

11. (2023盐城期末)如图2-2-21,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径$OC= 5cm$,弦$DE= 8cm$,则直尺的宽度为______3cm.

答案： 3cm

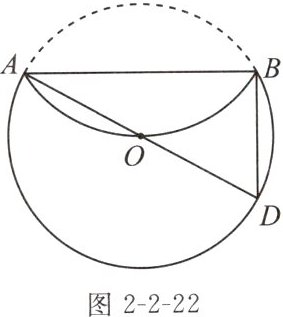
12. (2024常州月考)如图2-2-22,AD是$\odot O$的直径,将$\overset{\frown }{AB}$沿弦AB折叠后,$\overset{\frown }{AB}$刚好经过圆心O.若$BD= 6$,则$\odot O$的半径长是______6.

答案： 6

13. (2023南京玄武区期中)如图2-2-23,$\odot O$的半径是5,$\triangle ABC$的三个顶点A,B,C均在$\odot O$上,过圆心O分别作AB,BC,AC的垂线,垂足为E,F,G,连接EF,若$OG= 2$,则EF长为______$\sqrt{21}$.

答案： $\sqrt{21}$

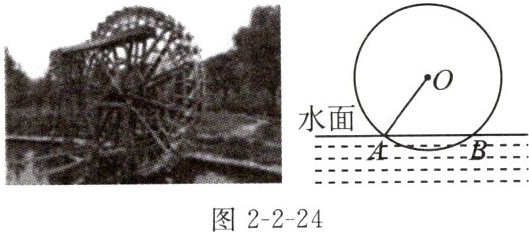
14. “筒车”是一种以水流作动力,取水灌田的工具,据史料记载,它发明于隋而盛于唐,距今已有1000多年的历史,是我国古代劳动人民的一项伟大创造.
如图2-2-24,“筒车”盛水筒的运行轨迹是以轴心O为圆心的圆,已知圆心O在水面上方,且当圆被水面截得的弦AB长为6m时,水面下盛水筒的最大深度为1m(即水面下方圆上部分一点距离水面的最大距离).
(1)求该圆的半径；
(2)若水面上涨导致圆被水面截得的弦AB的长从原来的6m变为8m(此时圆心O仍在水面上方),则水面上涨的高度为多少米？

答案：
解:
(1)如图,过点O作OD⊥AB,垂足为C,交⊙O于点D.
　　由题意可知,CD=1m,AB=6m.
　
∵OC⊥AB,AB=6m,
　
∴AC=BC=$\frac{1}{2}$AB=3m.
　　设⊙O的半径为rm,
　　即OA=OD=rm,OC=(r−1)m.
　　在Rt△AOC中,OC²+AC²=OA²,
　　即(r−1)²+3²=r²,
　　解得r=5,
　　即该圆的半径为5m.
　　　　
(2)设水面上升到如图EF的位置，则EF//AB,设OD与EF相交于点G.
∵EF//AB,OD⊥AB,
∴OD⊥EF,
∴EG=FG=$\frac{1}{2}$EF=$\frac{1}{2}$×8=4(m).
如图,连接OE.在Rt△EOG中,OE=5m,EG=4m,
∴OG=$\sqrt{OE²−EG²}$=3m,
∴CG=OC−OG=4−3=1(m).
即水面上涨的高度为1m.

1. 如图 2 - 2 - 25,AB,CD 是半径为 5 的⊙O 的两条弦,AB = 8,CD = 6,MN 是直径,AB⊥MN 于点 E,CD⊥MN 于点 F,P 为 EF 上的任意一点,则 PA + PC 的最小值为$7\sqrt{2}$。

答案： $ 7 \sqrt { 2 } $

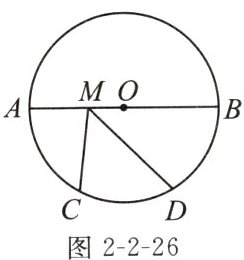
2. 如图 2 - 2 - 26,在⊙O 中,AB 为⊙O 的直径,AB = 12,C,D 是$\overset{\frown}{AB}$的三等分点,M 是 AB 上一动点,则 CM + DM 的最小值是______12。

答案： 12

3. 如图 2 - 2 - 27,在⊙O 中,直径 AB = 10,CD⊥AB 于点 E,CD = 8。F 是$\overset{\frown}{BC}$上的动点,且与点 B,C 不重合,对于每一个点 F,直径 AB 上总存在一点 P,使 PC + PF 的值最小,若这个最小值为 m,则 m 的取值范围是$ 8 ＜ m \leq 10 $。

答案： $ 8 ＜ m \leq 10 $